Háromszög Ábra Szög-Oldal-Szög (ASA)
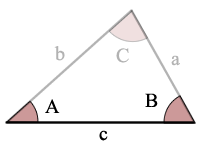
A = szög
B = szög B
C = szög C
egy = egy-egy oldalon
b = oldal b
c = c oldal
P = területet
s = félig területet
K = terület
r = sugár a beírt kör
R = sugár a körülírt kör
Számológép Használata
Minden számítási lehetőség, az alábbiak szerint rendelkezik al-golyók, amik a lista sorrendje alkalmazott módszerek ebben a kalkulátor megoldani ismeretlen irányból oldalon értékeket-beleértve a Szögek Összege egy Háromszög, Törvény Sines, valamint pitagorász elmélete, koszinusz tétel., Ezek nem az egyetlen szekvenciák, amelyeket felhasználhat az ilyen típusú problémák megoldására.
- Lásd még ezeket a trigonometriai számológépeket:
- a koszinusz számológép törvénye
Sines számológép törvénye
háromszög tételek megoldása
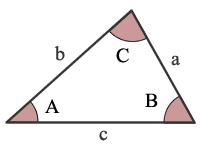
AAA szög, szög, szög, szög / h3>
a háromszög három szögének megadása nem azonosítja egyedileg az egyik háromszöget. Ezért a tringle két szögének meghatározása lehetővé teszi a harmadik szög kiszámítását.,
tekintettel a háromszög 2 szögének méretére, kiszámíthatja a harmadik szög méretét. A teljes egyenlő 180° vagy π radians.
C = 180° – A – B (fokban)
C = π – A – B (radiánban)
AAS szög, szög, oldal
tekintettel a 2 szög és 1 oldal méretére az adott szögek egyikével szemben, kiszámíthatja a fennmaradó 1 szög és 2 oldal méretét.
a szögek összege szabály segítségével keresse meg a másik szöget, majd
használja a szinuszok törvényét a másik két oldal mindegyikének megoldására.,
Asa szög, oldal, szög
tekintettel a 2 szög méretére és az oldal méretére, amely a 2 szög között van, kiszámíthatja a fennmaradó 1 szög és 2 oldal méretét.
a szögek összege szabály segítségével keresse meg a másik szöget, majd
használja a szinuszok törvényét a másik két oldal mindegyikének megoldására.,
ASS (vagy SSA) szög, Oldal, Oldal
tekintettel a 2 oldal méretére (a és c, ahol a < c) és az a szög méretére, amely nincs a két oldal között, a következő feltételektől függően ki lehet számítani a fennmaradó 1 oldal és 2 szög méretét.,f Cosines, hogy megoldja minden a másik két szög
a jelenlegi 2 teljes megoldások
Példa: 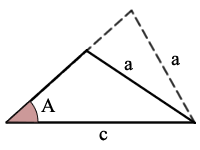
sin(A) = a/c, van egy lehetséges háromszög
a Jogot A Sines megoldani egy szög, C
használja a Szögek Összege Szabály, hogy megtalálja a másik szög, B
a Jogot A Sines, hogy megoldja az utolsó oldalon, a b
Példa: 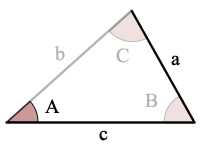
sin(A) > a/c, ott nem lehetséges, háromszög
Hiba Figyelmeztetés: sin(A) > a/c szóval nincsenek megoldások, illetve nem háromszög!,
példa:
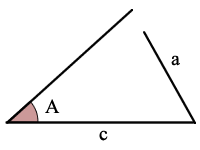
SAS is Side, Angle, Side
tekintettel a 2 oldal (c és a) méretére és a 2 oldal között lévő B szög méretére, kiszámíthatja a fennmaradó 1 oldal és 2 szög méretét.
használja a koszinusz törvényét a fennmaradó oldal megoldására, b
határozza meg, hogy melyik oldal, a vagy c, a legkisebb, és használja a szinusz törvényét az ellenkező szög, A vagy C méretének megoldására.,
használja a szögek összege szabályt, hogy megtalálja az utolsó szöget
az SSS Oldal, Oldal, oldal
a 3 oldal mérete alapján kiszámíthatja a háromszög mind a 3 szögének méretét.
használja a koszinusz törvényét a szögek megoldására. Ön is használja az összeg szögek szabály, hogy megtalálják a végső szöget, ha tudod, 2 közülük.,sin-1
koszinusz törvénye
Ha a, b és c az A, B és C szögekkel ellentétes háromszög lábainak hossza; akkor a koszinusz törvénye kimondja:
A2 = c2 + b2 – 2BC cos a, COS a megoldása, cos a = ( b2 + c2 – A2 ) / 2BC
b2 = A2 + c2 – 2CA cos B, cos B megoldása, cos B, cos B, cos B = ( C2 + a2 – b2 ) / 2CA
C2 = B2 + A2 – 2AB cos C, cos C = ( a2 + b2 – c2 ) / 2AB
megoldása, például egy szög, a = COS-1
egyéb háromszög jellemzői
háromszög kerülete, p = a + b + c
háromszög félperimeter, s = 0.,5 * (A + b + c)
háromszög terület, k = √
a háromszögbe írt kör sugara, r = √
a körülírt kör sugara a háromszög körül, R = (abc) / (4k)
referenciák/ további olvasás
Weisstein, Eric W. “ASS-tétel.”From MathWorld– A Wolfram Web Resource. Segg tétel.
Math is Fun-Solving SAS Triangles
















Vélemény, hozzászólás?