Ha egy háromszög szöge nem haladja meg a 180 fokot

1. Bevezetés

a háromszög szögei akár 180 fokot vagy $\pi$ radianokat is tartalmazhatnak? A válasz: “néha igen, néha nem”. Ez egy fontos kérdés? Igen, mert azt a megértést eredményezi, hogy vannak különböző geometriák, amelyek különböző axiómákon vagy “a geometria játékszabályain” alapulnak. Ez egy értelmes kérdés? Nos, nem, legalábbis addig nem, amíg nem állapodtunk meg a “szög” és a “szög” szavak jelentéséről, addig nem, amíg nem ismerjük a játék szabályait., Ebben a cikkben röviden megvitatjuk a mögöttes axiómákat, és egyszerű bizonyítékot adunk arra, hogy egy háromszög szögeinek összege az egységgömb felületén nem egyenlő $\pi$ – val, hanem $\pi$ plusz a háromszög területe. Fogjuk használni azt a tényt, hogy a terület a felület egy egység gömb $4\pi$.

2. A nagy tétel

mielőtt elmondhatnánk, hogy mi a háromszög, meg kell állapodnunk arról, hogy mit értünk pontok és vonalak alatt. Gömbgeometrián dolgozunk (szó szerint geometria egy gömb felületén)., Ebben a geometriában a tér a gömb felszíne, a pontok ezen a felületen pontok, a két pont közötti legrövidebb távolság pedig a két pontot tartalmazó nagy kör. Egy nagy kör (példáulaz egyenlítő) két egyenlő félgömbre vágja a gömböt. Ez a geometria nyilvánvaló alkalmazásokkal rendelkezik a földön lévő helyek és légi útvonalak közötti távolságokra.,

forgó gömb, amely nagy kört mutat

a két nagy kör közötti szög egy P pontban az euklideszi szög a körök irányai között (vagy szigorúan a P körök érintői között). Ez nem jelent nehézséget a földi navigációban, mert egy adott ponton úgy gondoljuk, hogy a szög két irány között olyan, mintha a Föld azon a ponton lapos lenne.

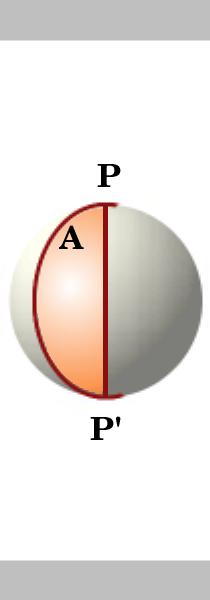
a lune a gömb felszínének egy része, amelyet két nagy kör határol, amelyek antipodális pontokon találkoznak., Először megvizsgáljuk a lune területét, majd egy másik nagy kört vezetünk be, amely a lune-t háromszögekre osztja.

4 lunes

Lemma.

a lune területe egy egység sugarú körön kétszerese a szögének, vagyis ha a lune szöge A, akkor a területe 2A. két nagy kör, amelyek metszenek a P és P antipodális pontokon. Az egységgömb felületének területe $ 4 \ pi$.,

a lunák területe arányos a P szögekkel, így az a szögű lune területe

${\frac{a}{2 \ pi} \ times {4 \ pi} = {2A}} $

1.gyakorlat.

melyek a többi 3 Luna területei? Ne a 4 területek összeadódnak $ 4 \ pi$?

Itt ellenőrizheti válaszait .

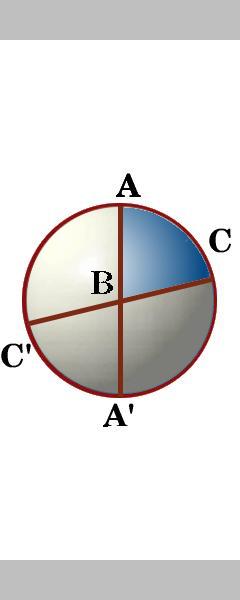
az ABC háromszög oldalai három nagy kör szegmensei, amelyek valójában a gömb felületét nyolc gömb alakú háromszögre vágják. A két nagy kör között az a ponton keresztül négy szög van., A címkét a szög belsejében ABC háromszög a szög, pedig hasonlóan a többi szögek ABC háromszög a szög B-szög C.

Forgó gömb mutatja, 8 háromszög

2. Gyakorlat

a Forgó gömb nevet a nyolc, háromszög, mondom, hogy nem ugyanazon a területen? Ellenőrizze a válaszokat itt .

tétel.

fontolja meg az ABC gömb alakú háromszöget az egységgömbön a, B és C szögekkel. ezután az ABC háromszög területe

a + B + C – $ \ pi$.,

az ábra egy olyan nézetet mutat, amely lefelé néz a féltekén, amelynek határa az AC-n keresztül vezet. Az 1. és 3. területet jelölő régiók a és C szögű lunák. Tekintsük a lunes-t B-n és B-n keresztül. Az ABC háromszög egybevág az A ‘ B ‘ C ‘háromszögvel, így a 2. területet jelölő, csokornyakkendő alakú árnyékolt terület, amely az ABC és a’ B ‘ háromszögek területeinek összege, egyenlő a B szögű lune területével, amely egyenlő a 2b-vel.,

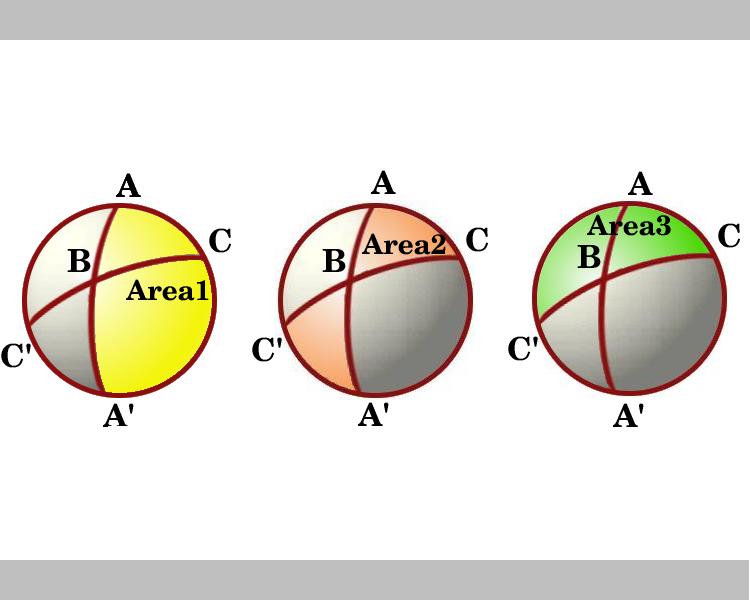
tehát az ábrán három Luna területét látjuk, és a lemma segítségével ezek a következők:

Terület 1 = 2a
Terület 2 = 2B
terület 3 = 2C

E három terület összeadásakor az ABC háromszög területét háromszor vesszük fel., Hence

3., Nem euklideszi geometria

néha forradalmi felfedezések nem más, mint valójában látni, mi volt az orrunk alatt minden alkalommal. Ez volt a helyzet a nem euklideszi geometria felfedezésével a tizenkilencedik században. Körülbelül 2000 évvel azután, hogy Euclid I.E. 325-ben megírta “elemeit”, az emberek megpróbálták bizonyítani a párhuzamos posztulátumot, mint a geometria tételét a többi axiómából, de mindig kudarcot vallottak, és ez egy hosszú történet., Eközben a matematikusok folyamatosan gömbgeometriát használtak, egy olyan geometriát, amely megfelel az euklideszi geometria többi axiómájának, és sok azonos tételt tartalmaz,de amelyben a párhuzamos posztulátum nem tart. Végig volt egy példa egy nem-euklideszi geometriára az orruk alatt.

Gondolj egy l vonalra és egy P pontra, nem L-re. a nagy kérdés az ,hogy ” hány vonalat lehet húzni p-n keresztül l-vel párhuzamosan?”Az euklideszi geometriában a válasz `pontosan egy”, ez pedig a párhuzamos posztulátum egyik változata., Ha a geometria minden háromszögének szögeinek összege $ \ pi $ Radian, akkor a párhuzamos posztulátum tart, és fordítva, a két tulajdonság egyenértékű.

a gömbgeometriában az általunk feltételezett alap axiómák (a játék szabályai) eltérnek az euklideszi geometriától – ez egy nem euklideszi geometria. Láttuk, hogy a gömbgeometriában a háromszögek szögei nem mindig adnak hozzá $ \ pi $ radianokat, így nem várnánk, hogy a párhuzamos posztulátum megmaradjon., A gömbgeometriában az egyenes vonalak (a legrövidebb távolság vagy a geodéziai vonalak)nagy körök, és a geometria minden vonala két pontban vág minden második vonalat. A párhuzamokkal kapcsolatos nagy kérdésre a válasz az, hogy ” ha van L vonalunk és P pontunk nem L-en, akkor az L vonallal párhuzamosan nincs p vonal.,”

a görög matematikusok (például Ptolemaiosz c 150) kiszámították a derékszögű gömb alakú háromszögek méréseit, és a gömb alakú trigonometria és az Arab matematikusok képleteivel dolgoztak (például Jabir ibn Aflah c 1125 és Nasir ed-din c 1250). Az ebben a cikkben tárgyalt képletet Harriot fedezte fel 1603-ban, amelyet Girard tett közzé 1629-ben. A téma további elemeit Saccerhi (1667 – 1733) fejlesztette ki.,

ez nagyrészt ensz-észre a 19-ik században fedezték fel hiperbolikus geometria, amely egy másik Nem-Euklideszi Geometria, ahol a párhuzamos posztulátum nem rendelkezik. A gömbgeometriában (más néven elliptikus geometriában) a háromszögek szögei több mint $\pi$ radianokat adnak, a hiperbolikus geometriában pedig a háromszögek szögei kevesebb mint $\pi$ radianokat adnak.

további olvasásért lásd Alan Beardon cikkét: “hány geometria van?”és Keith Carne” Strange Geometries ” című cikke ., Van néhány gyakorlati tevékenység, amelyet kipróbálhat magának, hogy felfedezze ezeket a geometriákat a http://nrich.maths.org/MOTIVATE/conf8/index.html