konvex és konkáv sokszögek

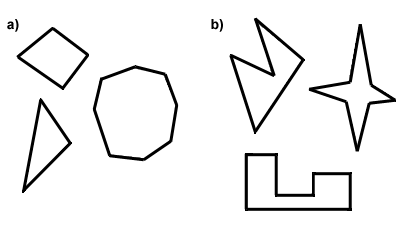
minden sokszög konvex vagy konkáv. A konvex és a konkáv sokszögek közötti különbség a szögek méretében rejlik. Ahhoz, hogy egy sokszög legyenkonvex, minden belső szögének kevesebbnek kell lennie, mint 180 fok. Ellenkező esetben a sokszögkoncávé. Egy másik módja annak, hogy erre gondoljunk: a konvexpoligon átlói mind a sokszög belsejében lesznek, míg a konkáv sokszög bizonyos átlói a sokszögen kívül, a külső oldalán fekszenek., Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.

Figure %: Convex and concave polygons

Regular Polygons

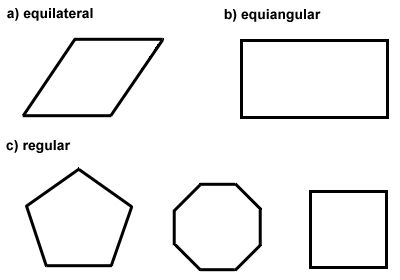
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., Ha egy sokszög mind egyenlő, mind egyenlő oldalúnégyszög, akkor rendszeres sokszögnek nevezik. A négyzet egy példa a rendszeres sokszögre. A szabályos sokszög középpontja az a pont, ahonnan a sokszög minden csúcsa egyenlő távolságra van. A rendszeres sokszögek különleges tulajdonságokkal rendelkeznek, amelyeket a következő szakaszban fogunk felfedezni. Az alábbiakban néhány példa az egyenlőtéglalapú, egyenlő oldalú és szabályos sokszögekre.,

Figure %: Equilateral, equiangular, and regular polygons

Congruent Polygons

One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.