Tartalom (Kattintson ugráshoz, hogy szakasz):
- a…
- Mármint
- Mód
- Medián
- Hogyan találja meg a jelent, a medián pedig módban kézzel.
- keresse meg az átlagos, medián és mód technológia:
- SPSS
- TI83
áttekintés
megragadt, hogyan lehet megtalálni az átlagos, medián, & mód statisztika?,
- az átlag egy adathalmaz átlaga.
- a mód az adatkészlet leggyakoribb száma.
- a medián a számok halmazának közepe.
A három közül az átlag az egyetlen, amely képletet igényel. Szeretem azt gondolni, hogy a másik szótár értelemben a szó (mint, ez azt jelenti, szemben a szép!). Ez azért van, mert a másik kettőhöz képest nem olyan könnyű dolgozni.,
utal, hogy emlékezzen a különbség
nehezen emlékszik a különbség az átlagos, medián és mód? Itt van néhány tipp, ami segíthet. Azt is nézd meg a tutorok Chegg.com (az első 30 perc ingyenes!).
- az “a la mode” egy francia szó, amely divatos ; a fagylalt népszerű kiszolgálására is utal. Tehát a ” mód ” a számok halmazának legnépszerűbb vagy divatos tagja. A szó mód is olyan, mint a legtöbb.,
- az “átlag” megköveteli az aritmetikát (az összes szám hozzáadása és az Osztás), tehát ez az “átlag”.
- ” medián “ugyanannyi betűvel rendelkezik, mint a”középső”.
még mindig nem biztos benne, hogy mi a különbség a három között? Nézze meg a videót, vagy olvassa tovább további információkért:
az átlagos
átlagos vs. medián
átlagos vs., Átlagos
specifikus “jelentése” általánosan használt statisztika
más típusú
átlagos vs medián
mindkettő olyan intézkedés, ahol a közepén egy adathalmaz fekszik (az úgynevezett “központi tendencia” a statisztika), de ezek általában különböző számok. Vegyük például ezt a számlistát: 10, 10, 20, 40, 70.
- az átlagot (informálisan az “átlagot”) úgy találjuk meg, hogy az összes számot összeadjuk, majd elosztjuk a készletben lévő elemek számával: 10 + 10 + 20 + 40 + 70 / 5 = 30.
- a medián úgy található meg, hogy a készletet a legalacsonyabbról a legmagasabbra rendeljük, és megtaláljuk a pontos közepet., A medián csak a középső szám: 20.
néha a kettő azonos szám lesz. Például az 1., 2., 4., 6., 7. adathalmaz a következő 1 + 2 + 4 + 6 + 7 / 5 = 4 és a medián (a középső) 4.
átlagos vs átlag: mi a különbség?
amikor először indult el a matematika, akkor valószínűleg azt tanították, hogy egy átlagos volt a “közepes” összeg egy sor számot. Összeadtad a számokat, osztva a lehetséges elemek számával és voilával! az átlagot kapod. Például 10, 5 és 20 átlaga:
10 + 6 + 20 = 36 / 3 = 12.,
The you started studying statistics and all of a hirtelen the “average” is now called the mean. Mi történt? A válasz az, hogy ugyanaz a jelentése(szinonimák).
hogy az említett, technikailag, a szó jelentése rövid a számtani átlag. Különböző szavakat használunk a statisztikákban, mert többféle eszköz létezik, és mindegyik különböző dolgokat csinál.
specifikus “jelentése” általánosan használt statisztika
akkor valószínűleg találkoznak ezeket a statisztika osztály., Nagyon szűk jelentésük van:
- a mintavételi Eloszlás átlaga: valószínűségi eloszlásokkal használják, különösen a központi Limit tételnél. Ez egy átlagos egy sor disztribúció.
- minta átlaga: a minta átlagos értéke.
- Population mean: az átlagos érték egy populációban.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1-3. Szerk. Princeton, NJ: van Nostrand, 1962.
egyéb típusok
vannak más típusú eszközök is, amelyeket a matematika különböző ágaiban használ., A legtöbb nagyon szűk alkalmazások területeken, mint a pénzügy vagy a fizika; ha az elemi statisztikák akkor valószínűleg nem fog működni velük.
Ezek a leggyakoribb típusok, amelyekkel találkozhat.
- súlyozott átlag.
- harmonikus középérték.
- geometriai átlag.
- aritmetikai-geometriai átlag.
- gyökér – átlagos négyzet átlag.
- Heróniai átlag.
- grafikus átlag
-
súlyozott átlag
ezek meglehetősen gyakoriak a statisztikákban, különösen populációk tanulmányozása során., Ahelyett, hogy minden adatpont egyformán hozzájárulna a végső átlaghoz, egyes adatpontok többet járulnak hozzá, mint mások. Ha az összes súly egyenlő, akkor ez megegyezik a számtani átlaggal. Vannak bizonyos körülmények, amikor ez helytelen információkat adhat, amint azt Simpson paradoxona is mutatja.
-
harmonikus átlag
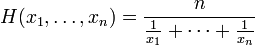
a harmonikus képlet.
megtalálásához:
- adja hozzá a számok dugattyúit a készletben., A kölcsönös megkereséshez fordítsa meg a frakciót úgy, hogy a számláló nevezővé váljon, a nevező pedig számlálóvá váljon. Például a 6/1 kölcsönös értéke 1/6.
- Oszd meg a választ a készletben lévő elemek számával.
- vegye figyelembe az eredmény reciprokját.
a harmonikus átlagot elég sokat használják a fizikában. Egyes esetekben az arányokat és arányokat figyelembe véve jobb átlagot ad, mint az aritmetikai átlag. A geometriában, a pénzügyekben és a számítástechnikában is megtalálható.,
-
aritmetikai-geometriai átlag
ezt leginkább a kalkulusban és a gépi számításban használják(azaz számos számítógépes számítás alapjaként). Egy ellipszis pereméhez kapcsolódik. Amikor először Gauss fejlesztette ki, a bolygók pályáinak kiszámításához használták. A számtani-geometriai (nem meglepő módon!) a számtani és geometriai átlagok keveréke. A matematika meglehetősen bonyolult, de itt viszonylag egyszerű magyarázatot talál a matematikáról.,
-
Root-Mean Square
nagyon hasznos olyan területeken, amelyek szinuszhullámokat tanulmányoznak, mint például az elektrotechnika. Ezt a típust kvadratikus átlagnak is nevezik. Lásd: Négyzetes Közép / Gyökér Átlagos Négyzet.
-
Heronian Mean
a geometriában használt piramis frustum térfogatának meghatározására. A piramis frustum alapvetően egy piramis, amelynek csúcsát levágták.
-
grafikus átlag
a metszővonal meredekségének másik neve: a két pont közötti átlagos változási sebességnek megfelelő.,
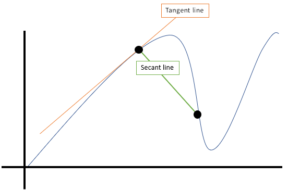
geometriai átlag
![]()
ennek a típusnak nagyon szűk és sajátos felhasználási területei vannak a pénzügyekben, a társadalomtudományokban és a technológiában. Tegyük fel például, hogy olyan készletekkel rendelkezik, amelyek az első évben 5% – ot, a második évben 20% – ot, a harmadik évben pedig 10% – ot keresnek. Ha szeretné tudni az átlagos megtérülési rátát, akkor nem használhatja az aritmetikai átlagot. Miért? Mert ha a megállapítás megtérülési ráta megszorozzuk, nem hozzátéve. Például az első évben megszorozzuk 1,05-tel.,
mi a mód?
az üzemmód a leggyakoribb szám egy készletben. Például ebben a számkészletben a mód 21:
21, 21, 21, 23, 24, 26, 26, 28, 29, 30, 31, 33
mi a Medián?
a medián az adatkészlet középső száma. A medián megtalálásához sorolja fel adatpontjait növekvő sorrendben, majd keresse meg a középső számot., A középső szám ez a beállítás 28, mint 4 szám alatt, 4 számok felett:
23, 24, 26, 26, 28, 29, 30, 31, 33
, Hogyan kell megtalálni az átlag, medián, valamint módban kézzel: Lépések
Hogyan találjuk meg az átlag, medián, illetve mód: MÓD
Hogyan találjuk meg az átlag, medián, illetve mód: ÉRTEM
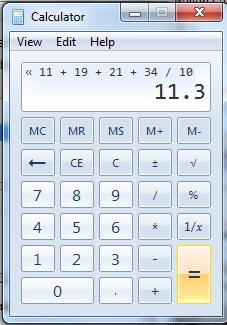
Elosztjuk az összeg a tételek száma, hogy megtalálja a jelent.
az átlag, a medián és a mód megtalálása: medián
Ha a 3. lépésben páratlan szám volt, LÉPJEN az 5.lépésre. Ha páros számod volt, menj a 6.lépésre.,
tipp: egynél több mód is lehet. Például az 1, 1, 5, 5, 6, 6 1, 5 és 6.
tetszik a magyarázat? Nézze meg a gyakorlatilag csaló statisztikák kézikönyve, amely több száz lépésről-lépésre megoldások, mint ez!
SPSS átlagos mód medián
az SPSS átlagos mód medián megtalálásához a frekvencia fület kell használnia. Kicsit ellentmondásosnak tűnik, de a leíró statisztikák lap nem ad lehetőséget a mód vagy a medián megtalálására.,
az SPSS nagyon hasonló felülettel rendelkezik a Microsoft Excel-hez. Ezért, ha korábban már használta a Microsoft Excel programot, gyorsan alkalmazkodik az SPSS-hez.
SPSS átlagos mód medián: lépések
nézze meg a videót, vagy olvassa el az alábbi lépéseket:
mintakérdés: keresse meg az SPSS átlagos mód mediánját a következő adatkészlethez: 20,23,35,66,55,66
1.lépés: Nyissa meg az SPSS-t. A ” mit szeretnél csinálni?”párbeszédpanel, kattintson a” írja be az adatokat “rádió gombot, majd kattintson az” OK.”Megnyílik egy új munkalap., Megjegyzés: ha kilépett az első Súgó képernyőről, előfordulhat, hogy nem látja ezt a lehetőséget. Ebben az esetben csak kezdje a 2.lépéssel.
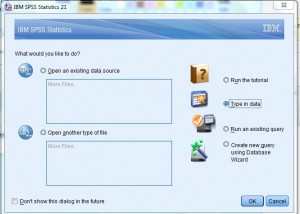
2.lépés: Írja be adatait a munkalapba. Az adatokat egy oszlopba vagy több oszlopba írhatja be, ha több adatkészlet van. Ebben a példában írja be 20, 23, 35, 66, 55, 66 az 1.oszlopba. Ne hagyjon szóközöket az adatok között (azaz ne hagyjon üres sorokat).
2. lépés: Kattintson az” Elemzés “gombra, vigye az egérmutatót a” leíró statisztikák “fölé, majd kattintson a “frekvenciák” gombra.,”
3. lépés: Kattintson a ” statisztika “elemre, majd jelölje be az” átlag”,” mód “és” medián ” négyzeteket. Kattintson kétszer a” Folytatás “gombra (a második ablakban válassza a” Nincs ” lehetőséget a diagram típusaként).
Megjegyzés: az SPSS egyes verzióiban előfordulhat, hogy csak egyszer kell kattintania a “Folytatás” gombra, és előfordulhat, hogy nem ad lehetőséget a diagram típusára.
a frekvencia eredmények kimenetként jelennek meg. A kimenet felső részén megjelenik az átlag, a mód és a medián.
ha lefelé görget, a frekvenciatábla megmutatja az üzemmódot is., Az üzemmódot a statisztikákban a legmagasabb frekvenciájú számként definiálják(ehhez a mintaadatkészlethez a leginkább megjelenő szám 66, két eredmény a frekvencia oszlopban).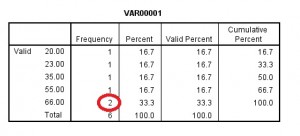
TI 83 átlag, medián és mód
a TI 83 átlag vagy TI 83 medián megtalálása az adatok listájából két módon valósítható meg: az adatok listájának megadásával vagy a kezdőképernyő használatával a parancsok beírásához., A lista funkció használata ugyanolyan egyszerű, mint az adatok bevitele a kezdőképernyőre, és előnye, hogy az adatokat más célokra is felhasználhatja, miután kiszámította az átlagot, a módot és a mediánt (például létrehozhat egy TI 83 hisztogramot).
a Lépéseket az átlag, Medián, illetve Mód a TI-83
nézze meg a videót a jelent, a medián, vagy olvassa el a lépések alatt (a mód, lásd ezt a levelet):
1. lépés: Írja be a fenti adatokat egy listába., Nyomja meg a STAT gombot, majd nyomja meg az ENTER billentyűt. Írja be az első számot (1250), majd nyomja meg az ENTER billentyűt. Folytassa a számok bevitelét, minden bejegyzés után nyomja meg az ENTER gombot.
2. lépés: Nyomja meg a STAT gombot.
3. lépés: Nyomja meg a jobb nyíl gombot a “Calc” kiemeléséhez.”
4. lépés: Nyomja meg az ENTER billentyűt az “1-Var statisztika” kiválasztásához, majd írja be a lista nevét. Például az L1 beírásához nyomja meg az and gombot .
5. lépés: Nyomja meg újra az ENTER billentyűt. A számológép visszaadja az átlagot, x. Az adatok listájához a TI 83 átlag 884,05 láb (3 tizedesjegyre kerekítve).
6. lépés: lefelé mutató nyíl, amíg meg nem jelenik a ” Med.,”Ez a TI 83 medián; a fenti adatok esetében a medián 813,05 láb.
megjegyzés: a TI-83 plus nem rendelkezik beépített üzemmód funkcióval, de miután belépett a listába, elég könnyű észrevenni az üzemmódot: ez csak a szám, amely a leggyakrabban fordul elő a készletben. Nem biztos? További információ a mód itt.
ennyi!
elvesztette az útikönyvet? Töltsön le egy újat itt a TI honlapján.
——————————————————————————
segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez?, A Chegg tanulmány segítségével lépésről-lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!
















Vélemény, hozzászólás?