A vektor magnitúdója (milyen hosszú), majd irány:
Itt van két vektor:

tudnak szorozni a “Dot Termék” (lásd Cross Product).,
ki Tudjuk számítani, hogy a Dot Termék két vektor így:

a · b = |a| × |b| × cos(θ)
, Ahol:
|a| a magnitúdó (hossza) a vector
|a b| a magnitúdó (hossza) a vektor b
θ közötti szög, b
Tehát szaporodnak a hossza egy alkalommal a hossza b, akkor szorozzuk meg a koszinusz a szög között, valamint b
VAGY meg lehet számolni, így:
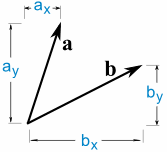
a · b = ax × bx + ay × által
Tehát szaporodnak az x, szorozza meg az y, majd adjunk hozzá.,
mindkét módszer működik!
és az eredmény egy szám (úgynevezett “skalár”, tehát tudjuk, hogy nem vektor).
Megjegyzés: használhatja a vektor Calculatorto segít.
miért cos (θ)?
OK, két vektor szorzásához érdemes a hosszúságukat együtt szaporítani, de csak akkor, ha ugyanabba az irányba mutatnak.,
tehát egy “pontot ugyanabban az irányban” hozunk létre, mint a másik, a cos(θ) szorzásával:
 |
 |
|
akkor szaporodnak !,
derékszögek
ha két vektor derékszögben van egymással, a ponttermék nulla.
Ez lehet egy praktikus módja annak, hogy megtudja, ha két vektor derékszögben.
három vagy több dimenzió
Ez mind jól működik 3 (vagy több) dimenzióban is.
és valóban nagyon hasznos lehet!
egyszer kipróbáltam egy ilyen számítást, de mind szögekben, mind távolságokban működött … nagyon nehéz volt, sok trigonometria volt benne, és fájt az agyam. A fenti módszer sokkal könnyebb.,
kereszttermék
A Dot termék skalár (rendes szám) választ ad, néha skalár terméknek nevezik.
de van olyan kereszttermék is, amely vektort ad válaszként, és néha vektorterméknek nevezik.

















Vélemény, hozzászólás?