Show Mobile Notice Show All Notes Hide All Notes
Szakasz 3-1 : Paraméteres Egyenletek, Görbék
ezen A ponton (mind a Matematika, illetve Matematika II.) már úgy nézett ki, szinte kizárólag a függvények formájában \(y = f\left( x \right)\) vagy \(x = h\a bal( y \right)\), valamint szinte az összes képletek kifejlesztettünk szükség, hogy a funkciók közül a két formában. A probléma az, hogy nem minden görbe vagy egyenlet, amelyet szeretnénk megnézni, könnyen beleesik ebbe a formába.
Vegyünk például egy kört. Elég könnyű leírni egy kör egyenletét, amelynek középpontja az Origó sugara \(r\).,
\
azonban soha nem leszünk képesek egy kör egyenletét egyetlen egyenletként leírni a fenti formák egyikében sem. Persze tudjuk megoldani a \(x\) vagy \(y\), mint a következő két képlet mutatja
\
de valójában két funkció mindegyik. Minden képlet adja a kör egy részét.
\
sajnos általában az egész körön dolgozunk, vagy egyszerűen nem mondhatjuk, hogy csak egy részét fogjuk dolgozni. Még akkor is, ha csak egy ilyen részre szűkíthetjük a dolgokat, a funkció még mindig meglehetősen kellemetlen.,
\
ezt a harmadik változót általában \(t\) jelöli (mint itt), de természetesen nem kell. Néha korlátozzuk az általunk használt \(t\) értékeket, máskor pedig nem. ez gyakran függ a problémától és attól, hogy mit próbálunk tenni.
annak érdekében, hogy egy parametrikus görbe pontosan megjelenjen, úgy teszünk, mintha egy nagy víztartály lenne, amely állandó mozgásban van, és egy ping-pong labdát dobunk a tartályba., A \(\left( {x,y} \right) = \left( {F\left( t \right),g\left( t \right)} \right)\) pont a ping-pong labda helyét jelöli a tartályban az időben \(t\), a parametrikus görbe pedig a ping-pong labda összes helyének nyomát fogja megjeleníteni. Ne feledje, hogy ez nem mindig helyes analógia, de kezdetben hasznos, hogy segítsen elképzelni, hogy mi a paraméteres görbe.
a paraméteres görbe rajzolása nem mindig könnyű dolog. Vessünk egy pillantást egy példára, hogy lássuk a parametrikus görbe rajzolásának egyik módját., Ez a példa azt is bemutatja, hogy miért ez a módszer általában nem a legjobb.
Ezen a ponton az egyetlen lehetőségünk egy paraméteres görbe rajzolására a \(t\) értékek kiválasztása, dugja be őket a parametrikus egyenletekbe, majd rajzolja meg a pontokat. Szóval dugjunk be néhány \(t\)’S-t.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Sajnos ezen a ponton nincs valódi válasz erre a kérdésre. Mi egyszerűen pick \(t\)’S, amíg nem vagyunk elég abban, hogy van egy jó ötlet, hogy mi a görbe néz ki. Ez a probléma a \(T\) “jó” értékeinek szedésével teszi ezt a parametrikus görbék vázlásának módszerét az egyik szegényebb választássá. Néha nincs más választásunk, de ha van választásunk, el kell kerülnünk.
a későbbi példákban egy alternatív grafikus módszert fogunk megvitatni, amely segít megmagyarázni, hogy a \(t\) értékeket hogyan választották ki.,
van még egy ötletünk, hogy megvitassuk, mielőtt ténylegesen vázoljuk a görbét. A parametrikus görbéknek mozgásirányuk van. A mozgás irányát A \(t\) növelésével adjuk meg. Tehát a paraméteres görbék ábrázolásakor olyan nyilakat is tartalmazunk, amelyek a mozgás irányát mutatják. Gyakran megadjuk a \(t\) értékét, amely adott pontokat a grafikonon is, hogy világossá tegyük a \(t\) értékét, amely adott pontot adott.
itt van ennek a paraméteres görbének a vázlata.
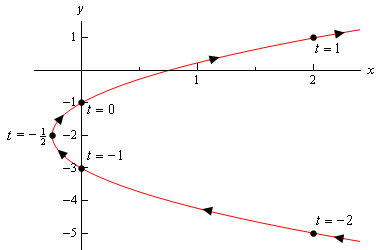
tehát úgy tűnik, hogy van egy parabola, amely jobbra nyílik.,
mielőtt befejeznénk ezt a példát, van egy kissé fontos és finom pont, amelyet először meg kell vitatnunk. Vegye figyelembe, hogy a vázlat egy részét a \(t = – 2\) és \(t = 1\) pontoknak megfelelő pontoktól jobbra helyeztük el, jelezve, hogy a vázlat részei ott vannak. Ha egyszerűen megállítottuk volna a vázlatot azokon a pontokon, akkor azt jelezzük, hogy a görbének nem volt része a pontoktól jobbra, és egyértelműen lesz. Csak nem számítottuk ki ezeket a pontokat.,
Ez jelentéktelennek tűnhet, de amint a következő példában látni fogjuk, ez fontosabb, mint gondolnánk.
a grafikon vázlatának sokkal könnyebb módja előtt először foglalkozzunk a paraméter korlátainak kérdésével. Az előző példában nem volt korlátozás a paraméterre. A paraméter korlátai nélkül a grafikon mindkét irányban folytatódik, amint azt a fenti vázlat mutatja.
a paraméternek gyakran vannak korlátai, ez azonban befolyásolja a parametrikus egyenletek vázlatát., Ennek a hatásnak a megtekintéséhez nézzük meg az előző példa enyhe változatát.
vegye figyelembe, hogy itt az egyetlen különbség a \(t\) határértékek jelenléte. Mindezek a korlátok azt mondják nekünk, hogy nem vehetünk semmilyen \(t\) értéket ezen a tartományon kívül. Ezért a parametrikus görbe csak a fenti görbe egy része lesz. Itt van a példa paraméteres görbéje.,
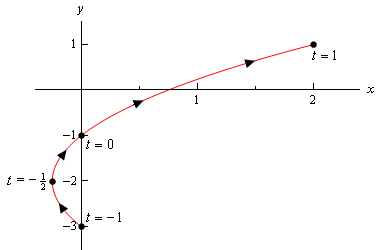
Észre, hogy ezzel a fantomkép kezdett, majd megállt a rajzot a pontok származó, a végén pont az a tartomány, a \(a t\)’s. Ezzel szemben a vázlat az előző példában, ahol volt egy részét a vázlat a “start”, majd a “vége” pontot, hogy mi számított.
ebben az esetben a görbe \(t = – 1\) – nál kezdődik, és \(t = 1\) – nál végződik, míg az előző példában a görbe valójában nem az általunk kiszámított legtöbb ponton indult el., Egyértelműnek kell lennünk a vázlatainkban, ha a görbe egy ponton indul/végződik, vagy ha ez a pont egyszerűen az első/utolsó volt, amelyet kiszámítottunk.
itt az ideje, hogy megnézzük a paraméteres görbe rajzolásának könnyebb módját. Ez a módszer azt a tényt használja fel, hogy sok, de nem minden esetben a parametrikus egyenletekből ténylegesen ki tudjuk zárni a paramétert, és csak \(x\) és \(y\) függvényt kapunk. Ezt néha algebrai egyenletnek nevezzük, hogy megkülönböztessük az eredeti parametrikus egyenletektől., Két kis probléma lesz ezzel a módszerrel, de könnyű lesz megoldani ezeket a problémákat. Fontos azonban megjegyezni, hogy nem mindig leszünk képesek erre.
a paraméter kiküszöbölésének módja a kapott parametrikus egyenletektől függ. Lássuk, hogyan lehet kiküszöbölni a parametrikus egyenletek halmazának paraméterét, amellyel eddig dolgoztunk.
a parametrikus görbe vázlata, miután megszüntettük a paramétert, meglehetősen egyszerűnek tűnik. Csak annyit kell tennünk, hogy grafikonozzuk az egyenletet,amelyet a paraméter kiküszöbölésével találtunk., Mint már említettük, két kis probléma van ezzel a módszerrel. Az első a mozgás iránya. A csak \(x\) és \(y\) egyenlet nem adja meg a parametrikus görbe mozgási irányát. Ez általában egy egyszerű probléma kijavítani azonban. Vessünk egy gyors pillantást a paraméteres egyenletek származékaira az utolsó példából. Ezek,
\
vegye figyelembe, hogy a \(x\) származék nem olyan hasznos erre az elemzésre, mivel mind pozitív, mind negatív lesz, ezért \(x\) mind növekszik, mind csökken a \(t\) értékétől függően., Ez nem sokat segít az irányban, mivel mindkét irányban a görbe követése mind növekvő, mind csökkenő \(x\) értéket mutat.
egyes esetekben csak az egyik egyenlet, például ez a példa adja meg az irányt, míg más esetekben bármelyik használható. Az is lehetséges, hogy bizonyos esetekben mindkét származékra szükség lenne az irány meghatározásához. Ez mindig függ az egyes paraméteres egyenletek halmazától.,
a paraméter kiküszöbölésével kapcsolatos második problémát legjobban egy példa szemlélteti, mivel a fennmaradó példákban belefutunk ebbe a problémába.
Oké, ez egy nagyon hosszú példa volt. A legtöbb ilyen típusú probléma nem olyan hosszú. Csak volt egy csomó, hogy megvitassák ebben az egy, így tudtuk, hogy egy pár fontos ötletet az útból. A többi példa ebben a szakaszban nem tart olyan sokáig, hogy menjen át.
most vessünk egy pillantást egy másik példára, amely bemutatja a parametrikus egyenletekkel kapcsolatos fontos elképzelést.,
tehát az utolsó két példában két parametrikus egyenletet láttunk, amelyek valamilyen módon ugyanazt a grafikont adták. Még, mert nyomon követhető a grafikon különböző számú alkalommal tényleg nem kell gondolni őket, mint a különböző paraméteres görbék legalább valamilyen módon. Ez olyan különbségnek tűnhet, amely miatt nem kell aggódnunk, de amint a későbbi szakaszokban látni fogjuk, ez nagyon fontos különbség lehet. Néhány későbbi szakaszban szükségünk lesz egy görbére, amelyet pontosan egyszer nyomon követünk.,
mielőtt továbblépnénk más problémákra, röviden ismerjük el, mi történik, ha a \(t\) – T nt-re változtatjuk az ilyen típusú parametrikus egyenletekben. Amikor csak szinuszokat és koszinuszokat tartalmazó parametrikus egyenletekkel foglalkozunk, és mindkettőnek ugyanaz az érvelése van, ha az argumentumot \(t\) – ról NT-re változtatjuk, egyszerűen megváltoztatjuk azt a sebességet, amellyel a görbe nyomon követhető. Ha \(n > 1\) növeljük a sebességet, és ha \(n < 1\) csökkentjük a sebességet.
vessünk egy pillantást még néhány példára.,
eddig a pontig láttunk olyan példákat, amelyek nyomon követnék a teljes grafikont, amelyet a paraméter kiküszöbölésével kaptunk, ha elég nagy \(t\) tartományt vettünk. azonban az előző példában most láttuk, hogy ez nem mindig lesz így. Ez több, mint lehetséges, hogy egy sor parametrikus egyenletek, amelyek folyamatosan nyomon követni csak egy része a görbe. Általában meg tudjuk határozni, hogy ez megtörténik-e, ha a \(x\) és \(y\) korlátokat keressük, amelyeket a parametrikus egyenlet kényszerít ránk.,
gyakran használunk parametrikus egyenleteket egy objektum vagy részecske útjának leírására. Vessünk egy példát erre.
Ezen a ponton egy kis figyelmeztetést kell adnunk. A bennük rejlő ötletek miatt olyan parametrikus görbékre koncentráltunk, amelyek többször visszahúzták a görbe részeit. Ne kerüljön azonban túlságosan bele abba az ötletbe, hogy ez mindig megtörténik. Sok, ha nem a legtöbb parametrikus görbe csak egyszer fog nyomozni. Az első, amit megnéztünk, jó példa erre. Ez a paraméteres görbe soha nem fogja megismételni önmagának egyetlen részét sem.,
van egy utolsó téma, amelyet ebben a szakaszban meg kell vitatni, mielőtt továbblépne. Eddig parametrikus egyenletekkel kezdtük, és megszüntettük a parametrikus görbe meghatározására szolgáló paramétert.
vannak azonban olyan idők, amikor a másik irányba akarunk menni. Adott egy függvény vagy egyenlet érdemes leírni egy sor parametrikus egyenletek rá. Ezekben az esetekben azt mondjuk, hogy paraméterezzük a funkciót.
ha példának vesszük a 4. és 5. példát, akkor ezt ellipszisek (és így körök) esetében is megtehetjük., Mivel az ellipszis
\
egy sor paraméteres egyenletek lenne,
\
Ez a sor paraméteres egyenletek fogja kideríteni, ki az ellipszis kezdve a lényeg \(\left( {a,0} \right)\), majd nyom egy óramutató járásával ellentétes irányba, majd kideríteni, hogy pontosan egyszer a tartományban \(0 \le t \le 2\pi \). Ez egy meglehetősen fontos paraméteres egyenlet, mivel az ellipszisekkel és/vagy körökkel foglalkozó egyes tantárgyakban folyamatosan használják.
minden görbe többféleképpen paraméterezhető. Az alábbiak bármelyike szintén paraméterezi ugyanazt az ellipszist.,
\
a \(\omega\) jelenléte megváltoztatja az ellipszis forgási sebességét, ahogy az 5. példában láttuk. Vegye figyelembe azt is, hogy az utolsó kettő az ellipsziseket az óramutató járásával megegyező irányú mozgással fogja nyomon követni (ezt érdemes ellenőrizni). Azt is vegye figyelembe,hogy nem mindegyik ugyanazon a helyen kezdődik (ha a \(t = 0\) – ra gondolunk, mint a kiindulási pontra).
az ellipszisnek természetesen sokkal több paramétere van, de megkapja az ötletet. Fontos megjegyezni, hogy minden paraméterezés egyszer nyomon követi a görbét, potenciálisan eltérő \(t\) tartományokkal., Minden paraméterezés különböző mozgási irányokkal foroghat, és különböző pontokon kezdődhet.
előfordulhat, hogy kell egy paraméterezzük egy ellipszis, hogy kezdődik egy adott helyen egy adott irányba, a mozgás, így most már tudjuk, hogy néhány munka, akkor írj le egy sor paraméteres egyenletek, hogy megadja neked a viselkedés maga után.
Most, írjunk le néhány egyéb fontos parametrizációk a megjegyzéseket iránya a mozgás, kiindulási pont, számos \(t\)’s egy trace (ha alkalmazandó) mindig igaz.,
először is, mivel egy kör nem más, mint egy ellipszis speciális esete, az ellipszis paraméterezését felhasználhatjuk egy kör paraméteres egyenleteinek a \(r\) sugara eredetére összpontosítva is. A kör paraméterezésének egyik lehetséges módja:
\ \
Ezen a ponton nem tűnik olyan hasznosnak egy ilyen funkció paraméterezésének elvégzése, de sok olyan eset van, amikor valójában könnyebb lesz, vagy akár szükség lehet arra is, hogy maga a funkció helyett a paraméterezéssel dolgozzon., Sajnos, szinte az összes ilyen esetek fordulnak elő a Calculus III tanfolyam.
















Vélemény, hozzászólás?