Show Mobile Notice Show All Notes Hide All Notes
4-11. szakasz: lineáris approximációk
ebben a szakaszban nem származékok, hanem egy függvény érintő vonalának alkalmazását fogjuk megvizsgálni. Természetesen ahhoz, hogy megkapjuk a tangens vonalat, származékokat kell vennünk, tehát valamilyen módon ez a származékok alkalmazása is.
\
vessen egy pillantást egy függvény és annak érintő vonalának alábbi grafikonjára.
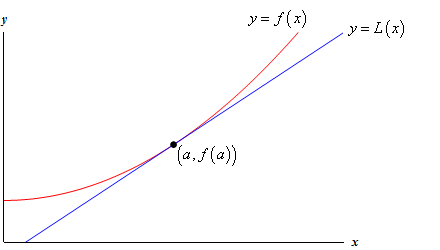
tehát miért tennénk ezt? Vessünk egy pillantást egy példára.,
A lineáris közelítések nagyon jó munkát végeznek a \(f\bal( x \jobb) \ értékek közelítésében, amíg “közel” \(x = a\) maradunk. Azonban minél távolabb van a \(x = A\) – tól, annál rosszabb lesz a közelítés. A fő probléma itt az, hogy milyen közel kell maradnunk a \(x = A\) – hoz, hogy jó közelítést kapjunk, mind az általunk használt függvénytől, mind az általunk használt \(x = a\) értéktől függ. Továbbá gyakran nem lesz könnyű megjósolni, hogy milyen messze van a \(x = A\) tudjuk kapni, és még mindig van egy ” jó ” közelítés.,
vessünk egy pillantást egy másik példára, amelyet néhány helyen meglehetősen erősen használnak.
Ez valójában egy kissé fontos lineáris közelítés. Az optikában ezt a lineáris közelítést gyakran használják a képletek egyszerűsítésére. Ez a lineáris közelítés is használják, hogy segítsen leírni a mozgás egy inga, rezgések egy húr.
















Vélemény, hozzászólás?