Black-Scholes Model: First Steps

div >

ma megnézzük a legnépszerűbb lehetőségeket árképzési modell. A Black Scholes modell, más néven a Black-Scholes-Merton módszer, egy matematikai modell árazási opció szerződések. A pénzügyi eszközök változásának becslésével működik. A technika azon a feltételezésen alapul, hogy az árak lognormális eloszlást követnek. Ennek alapján egy opció értéke származik.,

alkalmasabb az útvonalfüggetlen opciókra, amelyeket a befektetők nem gyakorolhatnak esedékességük előtt. Ez eltér a binomiális opció árképzési modelltől, amely kockázat-semleges módszer az útvonalfüggő opciók (például amerikai opciók) értékelésére.

elemzők és befektetők úgy vélik, hogy a fekete Scholes a modern pénzügyi elmélet egyik alapvető koncepciója.

Fischer Black és Myron Scholes 1973-ban mutatta be a Journal of Political Economy-ban, később pedig Robert Merton építette fel, a modell 1997-ben elnyerte a közgazdasági Nobel-díjat.,

a modell egy differenciálegyenletet követ, amelyet az opciók árainak megoldására használunk. A modell standard változatát használjuk az Európai stílusválasztásokhoz. A Black Scholes nem alkalmas az amerikai stílusú opciókra, mivel nem gondolja, hogy a befektetők ezeket a lehetőségeket a lejárati idő előtt bármikor gyakorolhatják.

a módszer feltételezi, hogy az alapul szolgáló állomány ára lognormális eloszlást követ, mivel nem lehet negatív. Az eloszlás, amelyre a modell támaszkodik, a Brown-mozgáson alapul, egy elmélet a természetben előforduló véletlenszerű jelenségek előrejelzésére.,

a modellt használjuk egy opció árának becslésére, a következő információk felhasználásával:

• az aktuális ár;
• a sztrájkár;
• lejáratig eltelt idő;
• várható osztalékhozam;
• várható kamatláb; és
• várható volatilitás.

kezdetben a modell nem veszi figyelembe az osztalékfizetések hatását. Ezért gyakran alkalmazkodik ehhez az alapul szolgáló eszköz osztalékfizetési dátumának meghatározásával., Az osztalékhozam csökkenti a jelenlegi részvényárfolyamot, mert az opciós jogosult lemond az osztalékról.

feltételezések

A Fekete Scholes modell csak akkor működik, ha bizonyos feltételezéseket teszünk.,s fordul elő az opció élettartama (ez a feltételezés volt az első modell, amely az elemzők azóta megszűnt hozzáadásával a osztalék hozam a modell képlete);

Fekete Scholes Formula

a modell formula matematikailag meglehetősen összetett, ami nem egy adott kérdés, mivel speciális eszközöket alkalmazhatunk számunkra annak kiszámításához. De még mindig elengedhetetlen megérteni, hogyan működik.,

kiszámításához az ár a vételi opció alatt a Black Scholes modell, akkor használja a következő egyenlet:

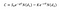
, Ahol:

• S0 a raktáron ár;
• e az exponenciális száma;
• q a osztalék hozam, százalékban;
• T a kifejezést (egy év lesz, T=1, míg hat hónapja lesz, T=0.,5);
• N (d1) a hívási opció deltája, ami azt jelenti, hogy a hívási ár változása a részvényárfolyam eltolódása felett;
• K a sztrájkár;
• r a kockázatmentes arány; és
• n(D2) annak a valószínűsége, hogy a jövőbeli részvényár magasabb lesz, mint a sztrájkár, annak valószínűsége, hogy élni fogunk a lehetőséggel.

az egyik oldalon a készlet ára szorozva a kumulatív standard normál eloszlása D1, a másik — a kötési ár, kedvezményes idő t, majd szorozva a kumulatív standard normál eloszlása D2.,

Amennyiben ki tudjuk számítani d1 meg d2, a következő képlet:

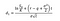
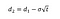
Ahol σ a volatilitás a hozamot az alapul szolgáló eszköz.,

Mi lehet alkalmazni, ugyanaz a logika, egy eladási opció:

Csatlakozz a Hírlevél INGYENES Excel Benchmark Elemzés Template

Példa a Black Scholes Számítás

ahhoz, Hogy jobban illusztrálja a koncepció mögött a Black Scholes Modell, akkor vessen egy pillantást a következő modell. Kezdjük a modell bemeneteivel., Mint fentebb említettük, a következő hat változóra van szükségünk a hívás kiszámításához, valamint az opcióértékek beállításához.

/ div >

ezután kiszámítjuk az opciók paramétereit. A d1-től kezdve 0, 39-et kapunk a modell feltételezéseinkből.

div >

annak kiszámításához egyszerűen átvisszük a D1 képletet az Excelbe.,

Following the same approach, we calculate d2, N(d1) and N(d2).

With those, we can calculate the Call Option Price and the Put Option Price.,

alkalmazhatjuk a call-put paritás szabályt annak ellenőrzésére, hogy képleteink és számításaink helyesek-e.

Most, hogy megvan a modell kiszámítja a vételi, illetve eladási opciók árak, menjünk egy lépéssel tovább, majd nézd meg, hogy a különböző bemeneti paraméterek befolyásolják az eredményeket a modell., Az Excel Adattábla funkcionalitása nagyszerű eszköz néhány érzékenységi elemzési táblázat elkészítéséhez változóink számára. Az Érzékenységelemző cikkünkben megtudhatja, hogyan kell használni az adattáblákat.

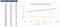
nézzük meg a részvényárfolyamot, ha 10 euróról 100 euróra változik, és hogyan befolyásolja a hívást és az értékeket. Észrevesszük, hogy a hívási opciónak nincs értéke, amíg a részvény ára eléri a 40 eurót. Látjuk a Put opció fordított értékét, ahol értéke nulla, ha a részvény ára 85 €fölé kerül.,

Ha ugyanazt az érzékenységi táblázatot készítjük a sztrájkárra, megfigyelhetjük a fordított kapcsolatot. Ahogy a sztrájk ára nő, a hívás értéke csökken, a Put érték pedig emelkedik.

nézzük meg a kockázatmentes arányt is., Ahogy növekszik, ez növeli a szükséges megtérülési arányt is. Ezt követően ez csökkenti a készletek értékét. Közvetlen kapcsolatot észlelünk, mivel a kockázatmentes arány növekszik, a hívás opció értéke is növekszik, míg a Put opció értéke csökkenti értékét.

ezt a megközelítést Követve, nyugodtan nézd meg a többi paraméterek, valamint hogyan befolyásolja a Lehetőség Értékek., A cikk végén letöltheti az Excel modellt,majd áttekintheti az érzékenységi elemzést.

letöltheti a példamodellt az Excelben az eredeti cikkben.

következtetés

fontos megjegyezni, hogy a fekete-Scholes-Merton modell elméleti koncepció. Arra használjuk, hogy megpróbáljuk megbecsülni a piac viselkedését. Amikor azonban az eredményeket felhasználjuk döntéshozatali folyamatunkban, meg kell értenünk a modellben szereplő alapvető feltételezéseket, valamint azt, hogy ez hogyan tér el a valóságtól.,

a képlet segített az opciók kereskedelmének népszerűbbé válásában, mivel kevésbé hasonlít a szerencsejátékra. Manapság a fekete Scholes különböző módosításai széles körben népszerűek, mint a kockázatkezelés alapvető stratégiái, amelyek a volatilitáshoz kapcsolódnak.

a cikk megosztásával megmutathatja támogatását kollégáival és barátaival.