férfiak. Valahogy úgy érzem, tetszik, amit mondasz.
Soc. És én, Meno, tetszik amit mondok.
Platón Meno
az egység négyzetének átlója hossza megegyezik a 2 négyzetgyökével.
az egység négyzetének átlójának hossza √2. Nos, ez nem igazán jó hír. Mindenki, aki valaha is találkozott a pitagorai tétel tudatában van annak a ténynek., Az egyenlő szárú derékszögű háromszögben az 1 hosszúságú lábakkal a hipotenusz a pitagorai tétel szerint – 12 + 12 = (hipotenusz)2-valóban hosszú √2. Ennek az oldalnak a motivációja nem annyira maga a tény, hanem a híres tétel igénybevétele nélkül történő bemutatásának módja. Valójában azt lehet vitatni, hogy a pitagorai tételt esetleg túlhasználták, lásd egy furcsa példát.
egy olyan érv, amely a Szókratész által Platón Menójában rajzolt alakra nyúlik vissza, maga Pythagoras is ismert lehetett, bár ez utóbbi egy évszázaddal korábban élt.,
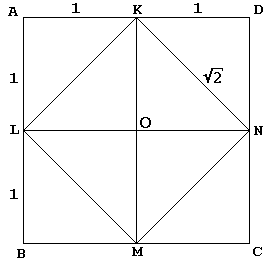
A párbeszédablakban Socrates szokásos módon egy fiatal rabszolgát vezet egy négyzet építéséhez, amely kétszerese az adott területnek:
az O középpontú klmn-t először átlói 4 egyenlő háromszögre vágják. Szókratész beágyazza KLMN egy nagyobb négyzet ABCD mintha tükrözi ezeket a háromszögeket minden annak hypotenuse. A rabszolga ezt követően beismeri – és ki nem tenné? – az a négyzet ABCD kétszer akkora, mint a négyzet KLMN.
Az igazat megvallva, Szókratész tér ABCD mért 4 oldalán, úgy, hogy a tér KLMN volt területe 8., Nyilvánvaló, hogy amikor a 2. oldal (tehát a 4. terület) négyzet alakú ABCD-vel kezdjük, a négyzet KLMN területe 2.
most, általában egy pozitív a számhoz, √a olyan szám, amelynek négyzete A:
(√a)2.
másrészt, minden tanuló területek tudja,, hogy a terület egy négyzet oldalán B egyenlő b2. Ebből következik, hogy az a területű négyzet oldala pontosan √A. arra a következtetésre jutunk,hogy a négyzet KLMN oldala megegyezik √2. Az egyik,
KN = √A.
az érv központi pontja az, hogy az ábrán a KN kettős szerepet játszik., Amellett, hogy a négyzet KLMN egyik oldala, a négyzet OKDN átlójaként is szolgál. Ez utóbbi természetesen egy egység négyzet, ami bizonyítja állításunkat.
(egy kicsit más szempontból ugyanazt az epizódot máshol említik.)
















Vélemény, hozzászólás?