egy polinom gyökerei

egy függvény gyökere vagy nullája olyan szám,amely a változó csatlakoztatásakor nullának teszi a függvényt. Így a polinom p(x) gyökerei x értékei, úgy, hogy P(x) = 0.

A Rational Zeros tétel

a Rational Zeros tétel kimondja:

a Rational Zeros tétel segítségével megtaláljuk a polinom összes racionális nulláját., Itt vannak a lépések:

  1. rendezze a polinomot csökkenő sorrendben
  2. írja le az állandó kifejezés összes tényezőjét. Ezek a p.
  3. összes lehetséges értéke, írja le a vezető együttható összes tényezőjét. Ezek mind a q lehetséges értékei.
  4. írja le a összes lehetséges értékét. Ne feledje, hogy mivel a tényezők negatívak lehetnek, a és – mindkettőt be kell vonni. Egyszerűsítse az egyes értékeket, majd húzza ki a másolatokat.,
  5. használjon szintetikus osztást a értékek meghatározásához, amelyekhez P() = 0. Ezek mind a P(x) racionális gyökerei.

példa: keresse meg a P(x) = x3-9x + 9 + 2×4-19×2 racionális nulláit.

ábra %: Synthetic Division

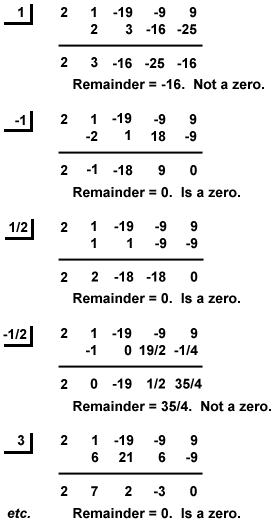
így a P(x) racionális gyökerei x = – 3, -1, 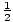és 3.

gyakran használhatjuk a racionális nullák tételét polinom faktorálására., A szintetikus divízió segítségével megtalálhatunk egy valódi a gyökeret, és megtalálhatjuk a hányadost, amikor P (x) x – a-val van felosztva. ezután szintetikus osztással megtalálhatjuk a hányados egy tényezőjét. Ezt a folyamatot addig folytathatjuk, amíg a polinom teljesen meg nem jelenik.