Triangle Figure Angle-côté-Angle (ASA)
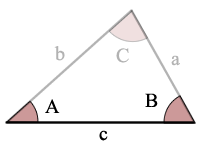
A = angle a
b = angle B
C = angle C
A = côté a
b = côté b
C = Côté C
P = périmètre
s = semi-périmètre
K = area
R = rayon du cercle inscrit
R = rayon du cercle circonscrit
utilisation de la calculatrice
chaque option de calcul, illustrée ci-dessous, comporte des sous-puces qui répertorient la séquence des méthodes utilisées dans cette calculatrice pour résoudre des valeurs d’angle et de côté inconnues, y compris la somme des angles dans un, Ce ne sont pas les seules séquences que vous pourriez utiliser pour résoudre ce type de problèmes.
- Voir aussi ces calculatrices de trigonométrie:
- calculateur de loi de cosinus
- calculateur de loi de sinus
résolution de théorèmes triangulaires
AAA est Angle, Angle, Angle
spécifier les trois angles d’un triangle N’identifie pas de manière unique un triangle. Par conséquent, la spécification de deux angles d’un tringle vous permet de calculer le troisième angle uniquement.,
étant donné les tailles de 2 angles d’un triangle, vous pouvez calculer la taille du troisième angle. Le total sera égal à 180° ou π radians.
C = 180° – A – B (en degrés)
c = π – A – B (en radians)
AAS est Angle, Angle, Side
étant donné la taille de 2 angles et 1 côté opposé à l’un des angles donnés, vous pouvez calculer les tailles des 1 angles et 2 côtés restants.
l’utilisation de la Somme des Angles Règle pour trouver l’autre angle, puis
utiliser La Loi des Sinus pour résoudre pour chacun des deux autres côtés.,
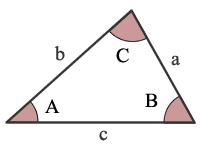
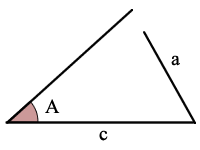
ASA est Angle, Side, Angle
étant donné la taille de 2 angles et la taille du côté qui se trouve entre ces 2 angles, vous pouvez calculer les tailles des 1 angles et 2 côtés restants.
l’utilisation de la Somme des Angles Règle pour trouver l’autre angle, puis
utiliser La Loi des Sinus pour résoudre pour chacun des deux autres côtés.,
ASS (ou SSA) est Angle, Side, Side
étant donné la taille de 2 côtés (a et c où a< c) et la taille de L’angle A qui n’est pas entre ces 2 côtés, vous pourriez être en mesure de calculer les tailles des 1 côtés et 2 angles restants, selon les conditions suivantes.,f Cosinus pour résoudre pour chacun des deux autres angles
présent 2 solutions complètes
Exemple: 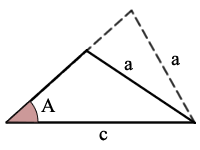
sin(A) = a/c, il y a un possible triangle
utiliser La Loi des Sinus pour résoudre un angle, C
l’utilisation de la Somme des Angles Règle pour trouver l’autre angle, B
utiliser La Loi des Sinus à résoudre pour le dernier côté, b
Exemple: 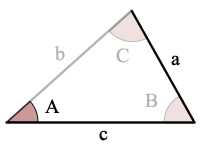
sin(A) > a/c, il n’y a pas possible triangles
un Avis d’Erreur: sin(A) > a/c, donc il n’y a pas de solutions et pas de triangle!,
exemple:
SAS est Side, Angle, Side
étant donné la taille de 2 côtés (c et a) et la taille de L’angle B qui se trouve entre ces 2 côtés, vous pouvez calculer les tailles des 1 côtés et 2 angles restants.
utilisez la loi des cosinus pour résoudre pour le côté restant, b
déterminez quel côté, a ou c, est le plus petit et utilisez la loi des sinus pour résoudre pour la taille de l’angle opposé, A ou C respectivement.,
l’utilisation de la Somme des Angles Règle pour trouver le dernier angle
SSS Côté, Côté, Côté
compte tenu de la taille des 3 côtés, vous pouvez calculer les tailles de tous les 3 angles du triangle.
utilisez la loi des cosinus pour résoudre les angles. Vous pouvez également utiliser la règle de la somme des Angles pour trouver l’angle final une fois que vous en connaissez 2.,sin-1
loi des cosinus
Si a, b et c sont les longueurs des jambes d’un triangle opposées aux angles A, B et c respectivement; alors la loi des cosinus indique:
a2 = c2 + b2 – 2BC cos A, résolvant pour cos A, cos A = ( b2 + c2 – a2 ) / 2BC
b2 = a2 + C2 – 2CA cos b, résolvant cos b, cos B = ( C2 + a2 – b2 ) / 2CA
C2 = B2 + A2 – 2AB Cos C, résolvant pour Cos C, Cos C = ( a2 + b2 – c2 ) / 2AB
résolvant, par exemple, pour un angle, A = cos-1
autres caractéristiques du triangle
périmètre du Triangle, P = A + B + C
périmètre, s = 0.,5 * (a + b + c)
Triangle area, K = √
rayon du cercle inscrit dans le triangle, r = √
rayon du cercle circonscrit autour du triangle, R = (abc) / (4K)
références/ lectures complémentaires
Weisstein, Eric W. « Ass Theorem. »De MathWorld A Une Ressource Web Wolfram. CUL Théorème.
Les mathématiques sont amusantes-résoudre des Triangles SAS
















Laisser un commentaire