géométrie: polygones

polygones convexes et concaves

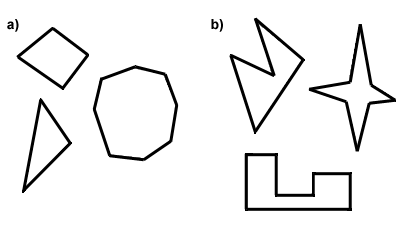
chaque polygone est convexe ou concave. La différence entre les polygones convexes et concaves réside dans les mesures de leurs angles. Pour qu’un polygone soit convexe, tous ses angles intérieurs doivent être inférieurs à 180 degrés. Sinon, le polygone estconcave. Une autre façon de penser, c’est ceci: les diagonales d’un convexpolygon seront tous dans l’intérieur du polygone, alors que certaines diagonales d’un polygone concave se trouvent à l’extérieur du polygone, sur l’extérieur., Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.

Regular Polygons

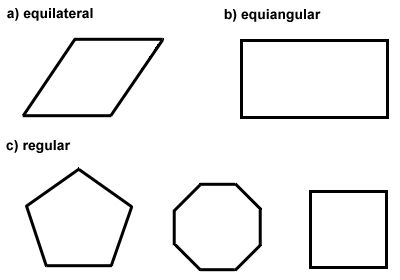
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., Lorsqu’un polygone est à la fois équilatéral et équiangulaire, on l’appelle un polygone régulier. Un carré est un exemple de polygone régulier. Le centre d’un polygone régulier est le point à partir duquel tous les sommets du polygone sont équidistants. Les polygones réguliers ont des propriétés spéciales que nous explorerons dans la section suivante. Voici quelques exemples de polygones équiangulaires, équilatéraux et réguliers.,

Congruent Polygons

One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.