tyypit vahvistimet, jotka olemme keskustelleet tähän mennessä ei toimi tehokkaasti radiotaajuuksien, vaikka ne ovat hyviä äänen taajuudet. Myös voitto näiden vahvistimet on sellainen, että se ei vaihdella taajuuden signaalin, laajalla alueella., Tämä mahdollistaa signaalin vahvistamisen yhtä hyvin eri taajuuksilla eikä salli tietyn halutun taajuuden valintaa hylätessään muita taajuuksia.
niin, tapahtuu tarve piiri, joka voi valita sekä vahvistaa. Niin, vahvistin piiri yhdessä valinta, kuten viritetty piiri tekee Viritetty vahvistin.
mikä on viritetty vahvistin?
viritetyt vahvistimet ovat vahvistimia, joita käytetään viritykseen. Viritys tarkoittaa valintaa., Joukossa joukko taajuuksia saatavilla, jos esiintyy tarvetta valita tietty taajuus, hylkäämällä kaikki muut taajuudet, tällainen prosessi kutsutaan valinta. Tämä valinta tehdään käyttämällä piiri kutsutaan viritetty piiri.
Kun vahvistin piiri on sen kuormitus korvattu kuulolla piiri, tällainen vahvistin voidaan kutsua Viritetty vahvistin piiri. Perus viritetty vahvistin piiri näyttää alla esitetyllä tavalla.
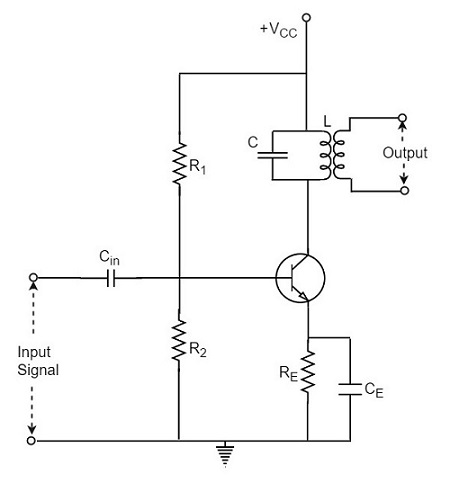
viritin piiri ei ole mitään, mutta LC-piiri, joka on kutsutaan myös kaikuva tai säiliö piiri. Se valitsee taajuuden., Viritetty piiri pystyy vahvistamaan signaalin kapealla taajuuskaistalla, joka on keskitetty resonanssitaajuudella.
Kun teemahotelli ic tasapainottaa teemahotelli kondensaattori, vuonna kuulolla piiri jossain taajuus, kuten taajuus voidaan kutsua kuin resonanssitaajuus. Se on merkitty fr.,
kaava resonanssi on
$$2 \pi f_L = \frac{1}{2 \pi f_c}$$
$$f_r = \frac{1}{2 \pi \sqrt{NM}}$$
Tyypit Viritetty Piirit
viritetty piiri voi olla Sarja viritetty piiri (Sarja kaikuva piiri) tai Rinnakkain viritetty piiri (samanaikaisesti kaikuva piiri) mukaan tyypin sen yhteys päävirtapiiri.
sarjan viritetty piiri
sarjaan kytketty induktori ja kondensaattori tekevät sarjan viritetyn piirin, kuten seuraavassa piirikaaviossa esitetään.,

Klo kaikuva taajuus, sarja kaikuva piiri tarjoaa alhainen impedanssi, joka mahdollistaa suuren virran. Sarjan resonanssipiiri tarjoaa yhä suurempi impedanssi taajuudet kaukana resonanssitaajuus.
rinnakkainen viritetty piiri
rinnakkain kytketty induktori ja kondensaattori tekevät rinnakkaisen viritetyn piirin, kuten alla olevassa kuvassa.
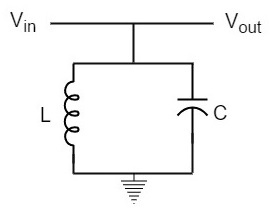
Klo kaikuva taajuus, samanaikaisesti kaikuva piiri tarjoaa korkea impedanssi, joka ei salli suuri virta läpi., Rinnakkainen resonanssipiiri tarjoaa yhä matalamman impedanssin taajuuksille kaukana resonanssitaajuudesta.
Ominaisuudet Samanaikaisesti Viritetty Piiri
taajuus, jolla rinnakkais resonanssi tapahtuu (eli reaktiivinen komponentti piirin virta tulee nolla) on nimeltään resonanssitaajuus fr. Viritetyn piirin tärkeimmät ominaisuudet ovat seuraavat.
Impedanssi
suhde jännitteeseen nykyinen linja on impedanssi kuulolla piiri., Impedanssi tarjoamia LC-piiri on antanut
$$\frac{Tarjontaa \: jännite}{Line yhtälö} = \frac{V}{I}$$
Klo resonanssi, linja virta kasvaa, kun impedanssi pienenee.
alla oleva kuva kuvaa rinnakkaisen resonanssipiirin impedanssikäyrää.
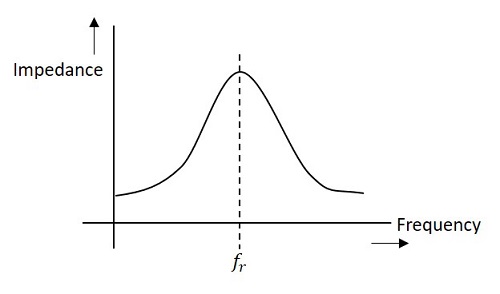
Impedanssi piiri pienenee arvojen ylä-ja alapuolella resonanssitaajuus fr. Siksi tietyn taajuuden valinta ja muiden taajuuksien hylkääminen on mahdollista.,
To obtain an equation for the circuit impedance, let us consider
Line Current $I = I_L cos \phi$
$$\frac{V}{Z_r} = \frac{V}{Z_L} \times \frac{R}{Z_L}$$
$$\frac{1}{Z_r} = \frac{R}{Z_L^2}$$
$$\frac{1}{Z_r} = \frac{R}{L/C} = \frac{C R}{L}$$
Since, $Z_L^2 = \frac{L}{C}$
Therefore, circuit impedance Zr is obtained as
$$Z_R = \frac{L}{C R}$$
Thus at parallel resonance, the circuit impedance is equal to L/CR.,
Piirin virta
Klo rinnakkais resonanssi -, piiri-tai line-nykyinen minä on antama jännite jaettuna piirin impedanssi Zr eli,
Line Nykyinen $I = \frac{V}{Z_r}$,
Missä $Z_r = \frac{L}{C, R}$
Koska Zr on erittäin korkea, linja nykyinen minä on hyvin pieni.
Laadukkaita Tekijä
rinnakkaista resonanssi piiri, terävyys resonanssi käyrä määrittää valikoivuus. Mitä pienempi käämin vastus on, sitä terävämpi resonanssikäyrä on., Siten Kelan induktiivinen reaktanssi ja vastus määrittävät viritetyn piirin laadun.
Kelan induktiivisen reaktanssin suhde resonanssissa sen vastukseen tunnetaan Laatutekijänä. Se on merkitty K.
$$Q = \frac{X_L}{R} = \frac{2 \pi f_r L}{R}$$
korkeampi arvo Q, terävämpi resonanssi käyrä ja parempi tulee olemaan valikoivuus.
Edut Kuulolla Vahvistimet
seuraavat ovat edut viritetty vahvistin.,
-
käyttö reaktiivisia komponentteja, kuten L-ja C -, minimoi tehon menetys, joka tekee viritetty tehokas vahvistimet.
-
valikoivuus ja vahvistusta haluttu taajuus on korkea, tarjoamalla korkeampi impedanssi klo resonanssitaajuus.
-
pienempi keräilijä toimittaa VCC tekisi, koska sen pieni vastus rinnakkain kuulolla piiri.
on tärkeää muistaa, että nämä edut eivät ole voimassa silloin, kun on olemassa suuri resistiivinen keräilijä ladata.,
viritetyn vahvistimen taajuusvaste
jotta vahvistin olisi tehokas, sen vahvistuksen pitäisi olla korkea. Tämä jännitevoitto riippuu β -, syöttöimpedanssi-ja keräilykuormasta. Viritetyn vahvistimen keräilykuorma on viritetty piiri.
jännite voitto tällainen vahvistin on annettu
Jännite voitto = $\frac{\beta Z_C}{Z_{in}}$
Missä ZC = tehokas kerääjä ladata ja Zin = input impedanssi vahvistimen.
ZC: n arvo riippuu viritetyn vahvistimen taajuudesta., Koska ZC on maksimi resonanssitaajuudella, vahvistimen voitto on maksimi tällä resonanssitaajuudella.
Kaistanleveys
taajuusalueella, jolla jännite voitto viritetty vahvistin laskee 70,7% maksimi voitto on nimeltään sen Kaistanleveys.
taajuuksien vaihteluväliä F1: n ja f2: n välillä kutsutaan viritetyn vahvistimen kaistanleveydeksi. Viritetyn vahvistimen kaistanleveys riippuu LC-piirin Q: sta eli taajuusvasteen terävyydestä. Q: n arvo ja kaistanleveys ovat kääntäen verrannollisia.,
alla oleva kuva kertoo viritetyn vahvistimen kaistanleveyden ja taajuusvasteen.
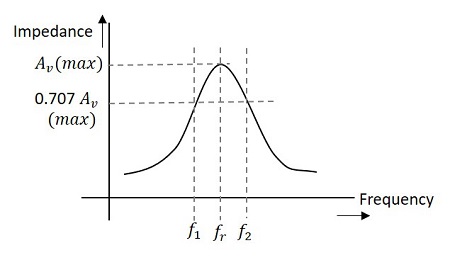
välinen Suhde, Q ja Kaistanleveys
laatukerroin Q kaistanleveys on määritelty suhde kaikuva taajuus, kaistanleveys, eli,
$$Q = \frac{f_r}{BW}$$
yleensä, käytännön piiri on sen Q-arvo on suurempi kuin 10.,
tämän ehdon, kaikuva taajuus, rinnakkais resonanssi saadaan kaavasta
$$f_r = \frac{1}{2 \pi \sqrt{NM}}$$
















Vastaa