Vektory jsou značně užitečné ve vědě popsat něco mají obě směr i velikost. Obvykle jsou kresleny pomocí špičatých šipek, jejichž délka bude představovat velikost vektoru. Quarterback přihrávka je jednoduchý příklad, protože má směr obvykle někde downfield a velikost. Někdy musíme zvládnout dva vektory společně pracovat na nějakém objektu. V takových případech jsou důležité úhly mezi těmito vektory., Toto téma bude vysvětlovat úhel mezi dvěma vektory vzorce, stejně jako příklady. Naučme se to!
koncept vektorů
mimo pole mohou být vektory použity k reprezentaci libovolného počtu fyzických objektů nebo činností. Příklad. Například vítr je vektorová veličina. Je to proto, že na jakémkoli daném místě má směr i velikost. Můžeme vytvořit mapu proudění vzduchu v libovolném okamžiku, pak, nakreslením větrných vektorů pro řadu různých geografických míst.
mnoho vlastností pohyblivých objektů je také druh vektorů., V kulečníkové kouli popisuje jeho vektor rychlosti jeho pohyb. Ukazuje směr vektorových šipek jako směr pohybu a délka vektoru představuje rychlost míče.
hybnost kulečníkové koule je také příkladem vektorového množství. Jak se rovná hmotnosti krát rychlost. Proto je vektor hybnosti kuličkových bodů ve stejném směru jako jeho vektor rychlosti. A velikost vektoru hybnosti bude násobícím produktem rychlosti míče a jeho hmotnosti.,
z hlediska matematiky je vektor jakýkoli objekt, který má definovatelnou velikost a směr. Protože vektory nejsou stejné jako standardní čáry nebo tvary, musíme použít některé speciální vzorce k nalezení úhlů mezi nimi.
Vzorec pro Úhel mezi Dvěma Vektory
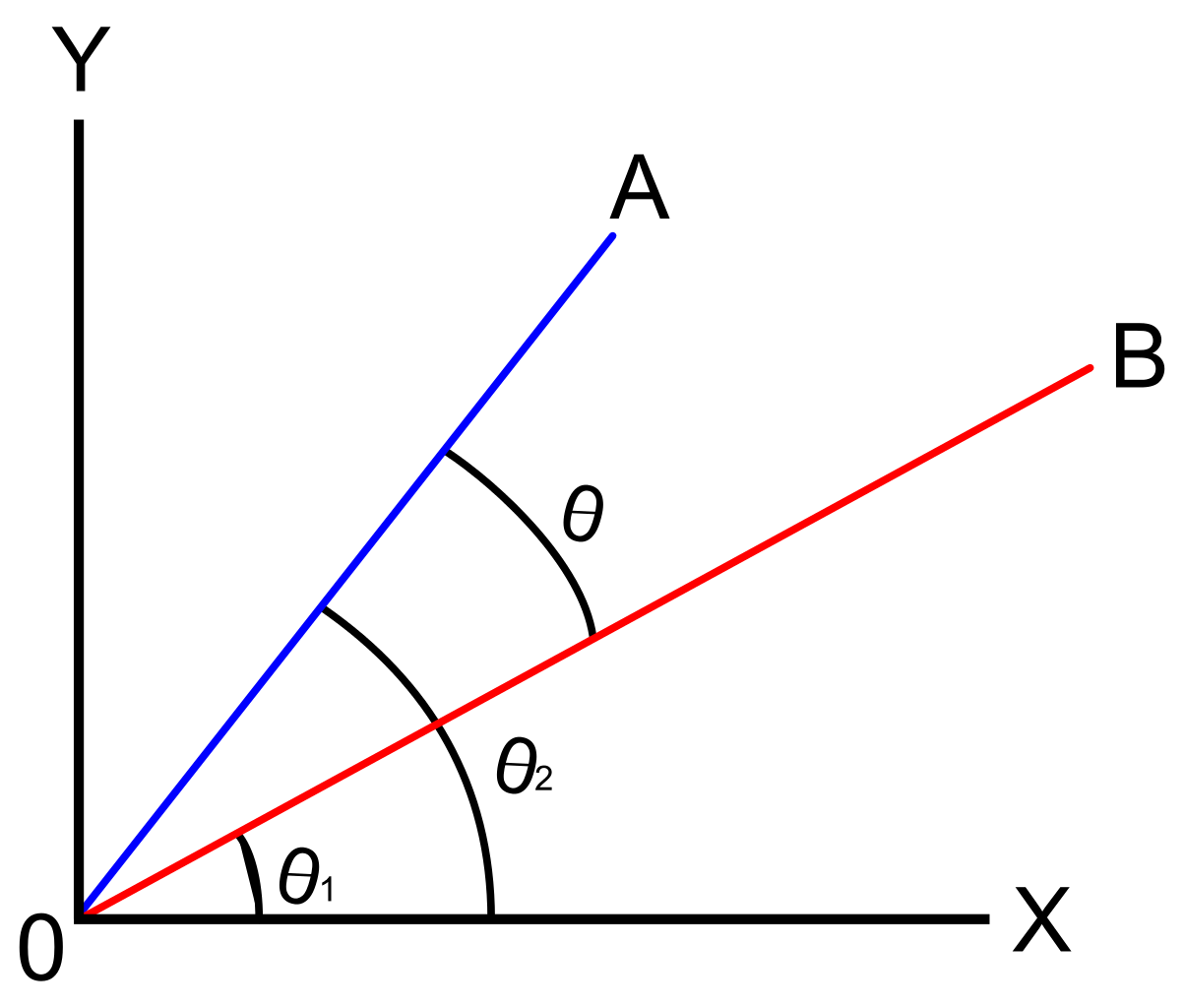
úhel mezi dvěma vektory bude odloženo o jeden bod, který se nazývá jako nejkratší úhel, pod kterým musíme otočit jeden z vektorů, na pozici co-directional s jiným vektorem.,
diskuse o směrových úhlech vektorů se zaměřuje na nalezení úhlu vektoru vzhledem k kladné ose x. To se zaměří na úhel mezi dvěma vektory ve standardní poloze. O vektoru se říká, že je ve standardní poloze, pokud jeho počátečním bodem je původ (0, 0).
Pokud se dva vektory předpokládají jako A A b, pak je vytvořená tečka definována jako a .b. předpokládejme, že tyto dva vektory jsou odděleny úhlem \ (\theta\). Chcete-li vědět, jaké je měření úhlu, vyřešíme pomocí daného vzorce:
známe produkt dot:
\(\vec{a}.,\vec{b} =|\vec{a} / / \vec{b} / cos \ theta\)
nyní je úhel mezi dvěma vektory vzorec:
\(\theta = cos^{-1} \ frac {\vec{a}.\vec{b}} {/\vec{a} / / \vec{b}/}\)
kde \ \ (theta\) je úhel mezi vektory a A b.
Řešených Příkladů pro Úhel mezi Dvěma Vektory Vzorec
Q. 1: Výpočet úhlu mezi dvěma vektory 3i + 4j – k a 2i – j + k.
Řešení: Nechat,
a = 3i + 4j – k a
b = 2i – j + k
Můžeme definovat skalární součin jako:
.b = (3i + 4J-k).(2i – j + K)
















Napsat komentář