vektor má velikost (jak dlouho to je) a směr:
Zde jsou dva vektory.

mohou být násobí pomocí „Dot Product“ (viz také vektorový součin).,
můžeme vypočítat Skalární součin dvou vektorů tímto způsobem:

a · b = |a| × |b| × cos(θ)
Kde:
|a| je velikost (délka) vektoru a,
|b| je velikost (délka) vektoru b.
θ je úhel mezi a a b
Takže můžeme vynásobit délku krát délka b, pak násobit cosinus úhlu mezi a a b
NEBO to můžeme spočítat takto:
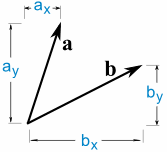
a · b = ax × bx + ay x
Tak vynásobíme x, vynásobte y, pak přidat.,
obě metody fungují!
a výsledkem je číslo (nazývané „skalární“, takže víme, že to není vektor).
Poznámka: Můžete použít vektor Calculatorto vám pomůže.
proč cos (θ) ?
OK, pro násobení dvou vektorů má smysl násobit jejich délky dohromady, ale pouze tehdy, když ukazují stejným směrem.,
Tak jsme se jeden „bod ve stejném směru“, jako ostatní vynásobením cos(θ):
 |
 |
|
| Vezmeme součástí , která leží vedle b |
Jako zářící světlo, abychom viděli, kde stíny leží |
PAK vynásobíme !,
pravé úhly
když jsou dva vektory v pravém úhlu k sobě, je bodový produkt nulový.
to může být užitečný způsob, jak zjistit, zda jsou dva vektory v pravém úhlu.
tři nebo více rozměrů
to vše funguje dobře i ve 3 (nebo více) rozměrech.
a může být skutečně velmi užitečné!
jednou jsem zkusil takový výpočet, ale pracoval jsem v úhlech a vzdálenostech … bylo to velmi těžké, zahrnovalo spoustu trigonometrie a můj mozek bolel. Výše uvedená metoda je mnohem jednodušší.,
Cross Product
Dot Product dává skalární (obyčejné číslo) odpověď a někdy se nazývá skalární produkt.
ale existuje také křížový produkt, který dává vektor jako odpověď a někdy se nazývá vektorový produkt.

















Napsat komentář