Pravděpodobnost pro válcování dvě kostky s šesti oboustranný dotssuch jako 1, 2, 3, 4, 5 a 6 bodů v každém umřít.

Když dvě kostky jsou hozeny současně, tedy počet událostí může být 62 = 36, protože každý die má 1 až 6 číslo na jeho tváře. Pak jsou možné výsledky uvedeny v následující tabulce.,
Pravděpodobnost – Ukázka prostor pro dvě kostky (výstupy):
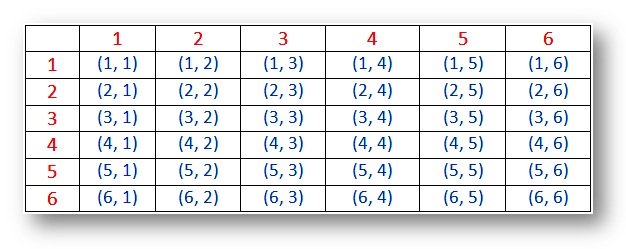
Poznámka:
(i) výsledky (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) a (6, 6) jsou tzv. dublety.
(ii) dvojice (1, 2) a (2, 1) jsou různé výsledky.
vypracované problémy zahrnující pravděpodobnost válcování dvou kostek:
1. Dvě kostky jsou válcovány. Nechť A, B, C jsou Události získání součtu 2, součtu 3 a součtu 4., Pak, ukázat, že
(i) je jednoduchá akce
(ii) B a C jsou složené události
(iii) a a B se vzájemně vylučují,
Řešení:
Jasně, máme
A = {(1, 1)}, B = {(1, 2), (2, 1)} a C = {(1, 3), (3, 1), (2, 2)}.
(i) Protože a sestává z jediného vzorkového bodu, je to jednoduchá událost.
(ii) protože B I C obsahují více než jeden bod vzorku, každá z nich je složená událost.
(iii) protože A ∩ B = ∅, A A B se vzájemně vylučují.
2. Dvě kostky jsou válcovány., A je událost, že součet čísel zobrazených na dvou kostkách je 5, A B je událost, že alespoň jedna z kostek se objeví 3.
jsou obě události (i) vzájemně se vylučující, (ii) vyčerpávající? Uveďte argumenty na podporu vaší odpovědi.
řešení:
když jsou dvě kostky válcované, máme n (S) = (6 × 6) = 36.
Nyní, = {(1, 4), (2, 3), (4, 1), (3, 2)},
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.
proto se A A B vzájemně nevylučují.,
(ii) také A ∪ B S S.
proto A A B nejsou vyčerpávající události.
Další příklady týkající se otázek o pravděpodobnosti házení dvou kostek.
3. Dvě kostky jsou hozeny současně.,) dostává kabátec
(v) dostane součet 8
(vi) získání částky dělitelné 5.
(vii) získání součet aspoň 11
(viii) dostat více 3 jako součet
(ix) získání celkem alespoň 10
(x) padne sudé číslo jako součet
(xi) získání hlavní číslo jako součet
(xii) dostává kabátec i čísla
(xiii) stále více z 2 na jeden zemřít a více 3 na druhou zemřít
Řešení:
Dvě různé kostky jsou hozeny současně je číslo 1, 2, 3, 4, 5 a 6 na jejich tvářích., Víme, že v jediném hozeném ze dvou různých kostek je celkový počet možných výsledků (6 × 6) = 36.
(i) získání šesti jako produktu:
nechte E1 = událost získání šesti jako produktu. Číslo, jehož produkt je šest bude E1 = = 4
Proto, pravděpodobnost získat šest jako produkt.
Počet příznivých výsledků
P(E1) = Celkový počet možných výsledků
= 4/36
= 1/9
(ii) získání sum ≤ 3:
E2 = událost, jak se dostat součet ≤ 3., Číslo, jehož součet ≤ 3 bude E2 = = 3
Proto, pravděpodobnost získat ‚sum ≤ 3‘
Počet příznivých výsledků
P(E2) = Celkový počet možných výsledků
= 3/36
= 1/12
(iii) získání částky nepřesahující 10:
E3 = událost, jak se dostat součet nejvýše 10. Číslo, jehož součet ≤ 10 bude E3 =
= 33
Proto, pravděpodobnost získat ‚sum ≤ 10‘
Počet příznivých výsledků
P(E3) = Celkový počet možných výsledků
= 33/36
= 11/12
(iv)získání kabátec:Ať E4 = událost, jak se dostat kabátec., Číslo, které kabátec bude E4 = = 6
Proto, pravděpodobnost získat to, ‚d‘,
Počet příznivých výsledků
P(E4) = Celkový počet možných výsledků
= 6/36
= 1/6
(v)dostane součet 8:
E5 = událost, jak se dostat součet 8. Číslo, které je součtem 8 bude E5 = = 5
Proto, pravděpodobnost získat to, ‚součet 8‘
Počet příznivých výsledků
P(E5) = Celkový počet možných výsledků
= 5/36
(vi)součet dělitelný 5:
E6 = událost, jak se dostat součet dělitelný 5., Číslo, jehož součet dělitelný 5 bude E6 = = 7
Proto, pravděpodobnost získat to, ‚součet dělitelný 5‘
Počet příznivých výsledků
P(E6) = Celkový počet možných výsledků
= 7/36
(vii)získání součet aspoň 11:
E7 = událost, jak se dostat součet aspoň 11. Události součet aspoň 11 bude E7 = = 3
Proto, pravděpodobnost získat to, ‚součet aspoň 11‘
Počet příznivých výsledků
P(E7) = Celkový počet možných výsledků
= 3/36
= 1/12
(viii) získání amultiple 3 jako součet:
Nechte E8 = událost, jak se dostat více 3 jako součet., Události násobkem 3 jako součet bude E8 = = 12
a Proto, pravděpodobnost získat ‚násobkem 3 jako součet
Počet příznivých výsledků
P(E8) = Celkový počet možných výsledků
= 12/36
= 1/3
(ix) získání totalof aspoň 10:
Nechte E9 = akce na získání celkem alespoň 10., Události celkem aspoň 10 bude E9 = = 6
Proto, pravděpodobnost získat ‚celkem aspoň 10‘
Počet příznivých výsledků
P(E9) = Celkový počet možných výsledků
= 6/36
= 1/6
(x) získání evennumber jako součet:
Nechte E10 = události, že padne sudé číslo jako součet., Události sudé číslo jako součet bude E10 = = 18
a Proto, pravděpodobnost získat ‚sudé číslo jako součet
Počet příznivých výsledků
P(E10) = Celkový počet možných výsledků
= 18/36
= 1/2
(xi) získání primenumber jako součet:
Nechte E11 = případě získání hlavní číslo jako součet., Události z prime číslo jako součet bude E11 = = 15
a Proto, pravděpodobnost získat ‚prvočíslo jako součet
Počet příznivých výsledků
P(E11) = Celkový počet možných výsledků
= 15/36
= 5/12
(xii) získání adoublet i čísla:
Nechte E12 = událost, jak se dostat kabátec i čísla., Události kabátec i čísla budou E12 = = 3
Proto, pravděpodobnost získat ‚kabátec i čísla.
Počet příznivých výsledků
P(E12) = Celkový počet možných výsledků
= 3/36
= 1/12
(xiii) získání amultiple 2 na jeden zemřít a více 3 na druhé die:
Nechte E13 = událost, jak se dostat více z 2 na jeden zemřít a více 3 na druhou zemřít., Události násobek 2 na jeden zemřít a více 3 na druhé smrti, bude E13 = = 11
a Proto, pravděpodobnost získat ‚násobkem 2 na jeden zemřít a více 3 na druhou zemřít‘
Počet příznivých výsledků
P(E13) = Celkový počet možných výsledků
= 11/36
4. Dvě hodiny jsou hozeny. Najít (i) šance ve prospěch získání částky 5, a (ii) theodds proti získání částky 6.
Řešení:
víme, že v jediném hodil dvě zemřít, celkový počet možných výsledků je (6 × 6) = 36.
nechť je vzorkovací prostor. Pak n (S) = 36.,
(i) šance na získání součtu 5:
nechť je E1 událostí získání součtu 5. Pak,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P(E1) = 4
Proto P(E1) = n(E1)/n(S) = 4/36 = 1/9
⇒ kurzy pro E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) šance na získání součtu 6:
Nechť E2 je událostí získání součtu 6. Pak,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
Proto P(E2) = n(E2)/n(S) = 5/36
⇒ šance proti E2 = /P(E2) = (1 – 5/36)/(5/36) = 31/5.
5., Dvě kostky, jedna modrá a jedna oranžová, jsou válcovány současně. Najděte pravděpodobnost získání
(i) stejných čísel na obou
(ii) se na nich objevují dvě čísla, jejichž součet je 9.,
Řešení:
možné výsledky,
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
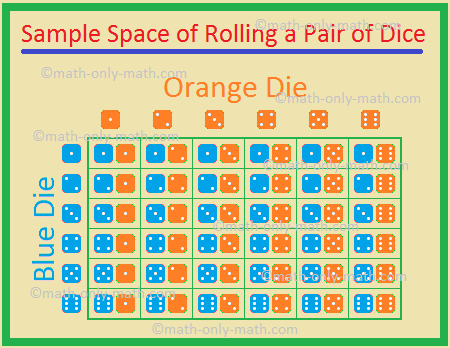
Proto, celkový počet možných výsledků = 36.,
(i) počet příznivých výsledků pro událost e
= počet výsledků, které mají stejná čísla na obou kostkách
= 6 .
Takže podle definice, P(E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Počet příznivých výsledků pro událost F
= Počet výsledků, ve které dvě čísla objevující se na nich mají součet 9
= 4 .
tedy podle definice P (F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
Tyto příklady se nám řešit různé typy problémů na základě pravděpodobnosti pro rollingtwo kostky.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Napsat komentář