Když úhly trojúhelníku nepřidávají až 180 stupňů

1. Úvod

do úhly trojúhelníku přidat až 180 stupňů nebo$ \ pi $ radians? Odpověď zní „někdy ano, někdy ne“. Je to důležitá otázka? Ano, protože to vede k pochopení, že existují různé geometrie založené na různých axiomech nebo „pravidlech hry geometrie“. Je to smysluplná otázka? No ne, alespoň ne, dokud se nedohodneme na významu slov ‚úhel‘ a ‚triangle‘, ne dokud neznáme pravidla hry., V tomto článku se budeme stručně diskutovat základní axiomy a dát jednoduchý důkaz, že součet úhlů v trojúhelníku na povrchu koule jednotky je rovna $\pi$, ale $\pi$ plus oblast trojúhelníku. Budeme používat skutečnost, že plocha povrchu jednotky koule je $ 4 \ pi$.

2. Velká věta

než můžeme říci, co je trojúhelník, musíme se dohodnout na tom, co máme na mysli body a čarami. Pracujeme na sférické geometrii (doslova geometrii na povrchu koule)., V této geometrii prostoru je povrch koule; body jsou body na povrchu, a řádek nejkratší vzdálenost mezi dvěma body je velký kruh, obsahující dva body. Velký kruh (jako rovník) řeže kouli na dvě stejné hemisféry. Tato geometrie má zřejmé aplikace na vzdálenosti mezi místy a leteckými trasami na Zemi.,

Rotující koule ukazuje velký kruh

úhel mezi dva velké kruhy v bodě P je Euklidovský úhel mezi směry kruhy (nebo přesněji mezi tečna k kruhy na P). To nepředstavuje žádné potíže s navigací na Zemi, protože v daném bodě myslíme na úhel mezi dvěma směry, jako by Země byla v tomto bodě plochá.

a lune je část povrchu koule ohraničená dvěma velkými kruhy, které se setkávají na antipodálních bodech., Nejprve zvážíme oblast lune a pak představíme další velký kruh, který rozdělí lune na trojúhelníky.

rotující koule zobrazující 4 lunes

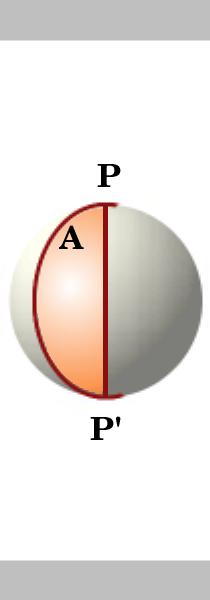
Lemma.

oblast lune na kruhu jednotky poloměr je dvakrát větší než jeho úhel, že je-li úhel lune je pak jeho plocha je 2A. Dva velké kruhy se protínají v antipodální bodů P a P‘ rozdělit sféry do 4 pondělí. Plocha povrchu jednotky koule je $ 4 \ pi$.,

oblasti lunes jsou úměrné jejich úhly na P tak v oblasti lune úhlu je A,

${\frac{A}{2\pi}\times {4\pi}= {2A}}$

Cvičení 1.

jaké jsou oblasti ostatních 3 lunes? Vaše 4 oblasti přidat až $ 4 \ pi$?

Zkontrolujte své odpovědi zde .

strany trojúhelníku ABC jsou segmenty tří velkých kruhů, které skutečně rozřezávají povrch koule na osm sférických trojúhelníků. Mezi dvěma velkými kruhy přes bod A jsou čtyři úhly., Označíme úhel uvnitř trojúhelníku ABC jako úhel, a podobně na jiných úhlů trojúhelníku ABC jako úhel B a úhel C.

Rotující koule zobrazuji 8 trojúhelníků,

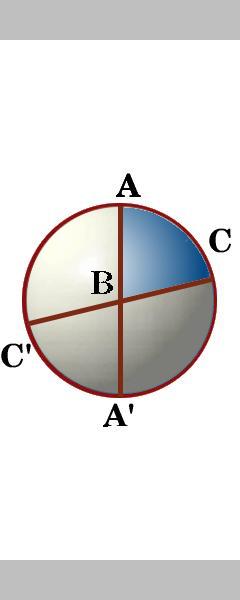
příklad 2

Rotující koule můžete jmenovat osm trojúhelníků a říci, zda některý z nich mají stejný obsah? Zkontrolujte své odpovědi zde .

věta.

zvažte sférický trojúhelník ABC na jednotce koule s úhly a, B A C. pak oblast trojúhelníku ABC je

a + B + C – $ \ pi$.,

diagram ukazuje pohled, který se dívá dolů na polokouli, která má čáru přes AC jako její hranici. Oblasti označené oblastí 1 a oblast 3 jsou lunes s úhly a A C, resp. Vezměme si lunes přes B A B‘. Trojúhelník ABC je shodný s trojúhelníkem A ‚ B ‚C‘, takže motýlek ve tvaru zastíněné oblasti, označené Oblast 2, což je součet ploch trojúhelníků ABC a’BC‘, je rovna oblasti lune s úhlem B, která je rovna 2B.,

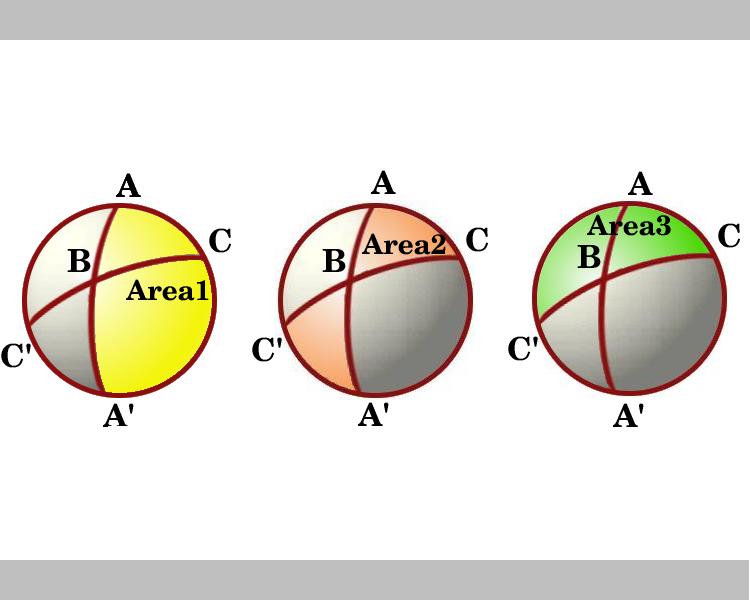
v diagramu vidíme, v oblasti tří lunes a, pomocí lemma, tyto jsou:

Oblast 1 = 2A
Oblast 2 = 2B
Oblast 3 = 2C

Při přidávání tyto tři oblasti můžeme zahrnout oblast trojúhelníku ABC třikrát., Hence

3., Non-Euklidovský Geometrie,

Někdy revoluční objevy nejsou nic víc, než skutečně vidět, co má pod nosem celou dobu. To byl případ objevu Non-euklidovské geometrie v devatenáctém století. Pro některé 2000 let poté, co Euclid napsal jeho ‚prvky‘ v 325 před naším letopočtem lidé se snažili dokázat paralelní postulát jako věta v geometrii z ostatních axiomů, ale vždy selhal, a toje dlouhý příběh., Mezitím matematici používali sférickou geometrii po celou dobu, geometrii, která poslouchá další axiomy euklidovské geometrie a obsahuje mnoho stejných vět, ale ve kterých paralelní postulát nedrží. Po celou dobu měli příklad Non-euklidovské geometrie pod nosem.

pomyslete na řádek L a bod P ne na L. velkou otázkou je: „kolik řádků lze protáhnout P rovnoběžně s L?“V euklidovské geometrii je odpověď“ přesně jedna “ a to je jedna verze paralelního postulátu., Pokud je součet úhlů každého trojúhelníku v geometrii$ \ pi $ radians, pak paralelní postulát drží a naopak, obě vlastnosti jsou ekvivalentní.

v sférické geometrii se základní axiomy, které předpokládáme (pravidla hry), liší od euklidovské geometrie – Jedná se o Neeuklidovskou geometrii. Viděli jsme, že v sférické geometrii úhly trojúhelníků ne vždy sčítají až$ \ pi $ radiány, takže bychom neočekávali, že paralelní postulát bude držet., V sférické geometrii jsou přímky (čáry nejkratší vzdálenosti nebo geodézie) skvělé kruhy a každá čára v geometrii řeže každou druhou čáru ve dvou bodech. Odpověď na velkou otázku o paralelách je`pokud máme čáru L a bod P ne na L, pak neexistují žádné čáry přes P rovnoběžné s čárou L.,“

řečtí matematici (například Ptolemaios c 150) počítačová měření pravoúhlý sférické trojúhelníky a pracoval s vzorců sférické trigonometrie a Arabských matematiků (například Jabir ibn Aflah c 1125 a Nasir ed-din c, 1250) prodloužený práci ještě dále. Vzorec diskutovaný v tomto článku byl objeven Harriotem v roce 1603 a publikován Girardem v roce 1629. Další náměty byly vyvinuty Saccerhi (1667 – 1733).,

to vše šlo do značné míry un-všiml 19. století objevitelé hyperbolické geometrie, což je další Non-euklidovské geometrie, kde paralelní postulát nedrží. V sférické geometrii (nazývané také eliptická geometrie) úhly trojúhelníků přidávají až více než $\pi$ radians a v hyperbolické geometrii úhly trojúhelníků přidávají až méně než $\pi$ radians.

pro další čtení viz článek Alana Beardona ‚ kolik geometrií existuje?’a článek Keitha Carna ‚podivné geometrie‘., Tam jsou některé praktické činnosti, které si můžete vyzkoušet sami prozkoumat tyto geometrie dále lze nalézt na http://nrich.maths.org/MOTIVATE/conf8/index.html