Konvexní a Konkávní Polygony

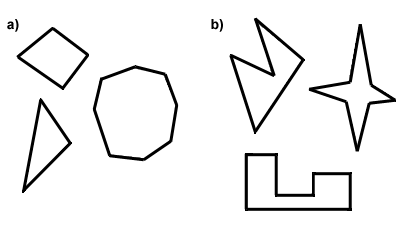
Každý polygon je buď konvexní, nebo konkávní. Rozdíl mezi konvexními a konkávními polygony spočívá v měření jejich úhlů. Pro polygon beconvex musí být všechny jeho vnitřní úhly menší než 180 stupňů. Jinak je polygonkonkáve. Dalším způsobem, jak o tom přemýšlet, je toto: úhlopříčky konvexpolygonu budou všechny v interiéru mnohoúhelníku, zatímco některé úhlopříčky konkávního mnohoúhelníku budou ležet mimo mnohoúhelník, na jeho exteriéru., Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.

Figure %: Convex and concave polygons

Regular Polygons

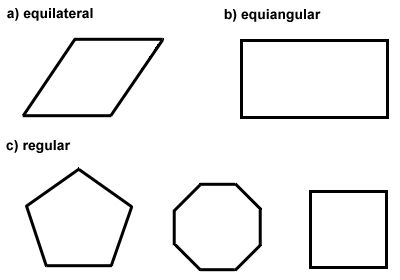
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., Když je polygon rovnostranný i rovnostranný, nazývá se pravidelným polygonem. Čtverec je příkladem pravidelného polygonu. Střed pravidelného polygonu je bod, ze kterého jsou všechny vrcholy polygonu stejně vzdálené. Pravidelné polygony mají speciální vlastnosti, které prozkoumáme v další části. Níže jsou uvedeny některé příklady rovnoúhlých, rovnostranných a pravidelných polygonů.,

Figure %: Equilateral, equiangular, and regular polygons

Congruent Polygons

One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.