Diferenciální počet II – Parametrické Rovnice a Křivky

Zobrazit Mobilní Oznámení, Zobrazit Všechny Poznámky, Skrýt Všechny Poznámky,

Část 3-1 : Parametrické Rovnice Křivky

K tomuto bodu (v obou diferenciální počet i a integrální počet II) podívali jsme se téměř výhradně na funkce ve tvaru \(y ‚ = f\left( x \right)\) nebo \(x = h\left( a \right)\) a téměř všechny vzorce, které jsme vyvinuli požadovat, aby funkce byla v jedné z těchto dvou forem. Problém je v tom, že ne všechny křivky nebo rovnice, na které bychom se chtěli podívat, snadno spadají do této formy.

Vezměte například kruh. Je snadné zapsat rovnici kruhu vystředěného na počátku s poloměrem \(r\).,

\

nikdy však nebudeme schopni napsat rovnici kruhu dolů jako jednu rovnici v žádné z výše uvedených forem. Určitě můžeme vyřešit pro \(x\) nebo \(y\), protože následující dva vzorce ukazují

\

, ale ve skutečnosti jsou v každé z nich dvě funkce. Každý vzorec dává část kruhu.

\

bohužel obvykle pracujeme na celém kruhu, nebo prostě nemůžeme říci, že budeme pracovat pouze na jedné části. I když můžeme zúžit věci pouze na jednu z těchto částí, funkce je stále často docela nepříjemná pro práci.,

\

tato třetí proměnná je obvykle označována \(t\) (jako jsme to udělali zde), ale nemusí to být samozřejmě. Někdy budeme omezovat hodnoty \(t\), které budeme používat a jindy nebudeme. to bude často záviset na problému a na tom, co se snažíme dělat.

Chcete-li pomoci vizualizovat, jen to, co parametrické křivky, je předstírat, že máme velkou nádrž vody, která je v neustálém pohybu a spustíme ping pong míč do nádrže., Bod \(\left( {x,y} \right) = \left( {f\left( t \right),g\left( t \right)} \right)\), pak bude představovat umístění ping pong míč v nádrži v čase \(t\) a parametrická křivka bude trasování všech místech ping pong míček. Všimněte si, že to není vždy správná analogie, ale je užitečné zpočátku pomoci vizualizovat, co je parametrická křivka.

načrtnutí parametrické křivky není vždy snadné. Podívejme se na příklad, abychom viděli jeden způsob načrtnutí parametrické křivky., Tento příklad také ilustruje, proč tato metoda obvykle není nejlepší.

Příklad 1 načrtněte parametrickou křivku pro následující sadu parametrických rovnic. \

Zobrazit řešení

v tomto okamžiku je naší jedinou možností pro načrtnutí parametrické křivky vybrat hodnoty \(t\), zapojit je do parametrických rovnic a poté vykreslit body. Tak, pojďme zapojit některé \(t\)’s.,x\)

\(y\) -2 2 -5 -1 0 -3 \( – \frac{1}{2}\) \( – \frac{1}{4}\) -2 0 0 -1 1 2 1

The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Bohužel v tomto bodě neexistuje žádná skutečná odpověď na tuto otázku. Jednoduše si vybereme \(t\), dokud nebudeme docela přesvědčeni, že máme dobrou představu o tom, jak vypadá křivka. Právě tento problém s výběrem „dobrých“ hodnot \(t\) činí tuto metodu skicování parametrických křivek jednou z chudších možností. Někdy nemáme na výběr, ale pokud máme na výběr, měli bychom se tomu vyhnout.

v pozdějších příkladech budeme diskutovat o alternativní grafové metodě, která pomůže vysvětlit, jak byly tyto hodnoty \(t\) vybrány.,

máme ještě jeden nápad diskutovat, než skutečně načrtneme křivku. Parametrické křivky mají směr pohybu. Směr pohybu je dán zvýšením \(t\). Takže při vykreslování parametrických křivek zahrnujeme také šipky, které ukazují směr pohybu. Často dáme hodnotu \(t\), která dala konkrétní body na grafu, abychom objasnili hodnotu \(t\), která dala tento konkrétní bod.

zde je náčrt této parametrické křivky.

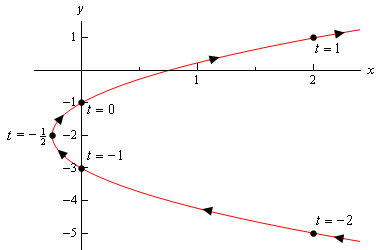
takže to vypadá, že máme parabolu, která se otevírá doprava.,

než tento příklad ukončíme, existuje poněkud důležitý a jemný bod, o kterém musíme nejprve diskutovat. Všimněte si, že jsme určitě zařadit část skici, doprava z bodů, který odpovídá \(t = – 2\) a \(t = 1\) značí, že tam jsou části skici. Kdybychom prostě zastavili náčrt v těch bodech, naznačujeme, že na těchto bodech nebyla žádná část křivky vpravo a jasně bude. Jen jsme nepočítali žádný z těch bodů.,

to se může zdát jako nedůležitý bod, ale jak uvidíme v dalším příkladu, je to důležitější, než bychom si mohli myslet.

Před řešení mnohem jednodušší způsob, jak nakreslit tento graf pojďme se nejprve zabývat otázkou omezení na parametr. V předchozím příkladu jsme neměli žádné limity parametru. Bez omezení parametru bude graf pokračovat v obou směrech, jak je znázorněno na náčrtu výše.

často však budeme mít limity parametru, což ovlivní náčrt parametrických rovnic., Chcete-li vidět tento efekt, podívejme se na malou změnu předchozího příkladu.

příklad 2 načrtněte parametrickou křivku pro následující sadu parametrických rovnic. \

Zobrazit řešení

Všimněte si, že jediným rozdílem je přítomnost limitů na \(t\). Všechny tyto limity nám říkají, že nemůžeme vzít žádnou hodnotu \(t\) mimo tento rozsah. Proto bude parametrická křivka pouze částí výše uvedené křivky. Zde je parametrická křivka pro tento příklad.,

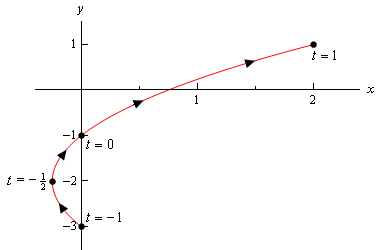
Všimněte si, že s tímto skici jsme začali a přestali skici přímo na body pocházející z koncových bodech rozsahu \(t\). Tento kontrast s náčrtek v předchozím příkladu, kde jsme měli část náčrt na pravé straně „start“ a „end“ body, které jsme počítán.

V tomto případě křivka začíná na \(t = – 1\) a končí na \(t = 1\), vzhledem k tomu, že v předchozím příkladu křivky nezačal ve správný většina bodů, které jsme počítán., V našich náčrtcích musíme být jasní, pokud křivka začíná/končí přímo v bodě, nebo pokud byl tento bod jednoduše první/poslední, který jsme vypočítali.

nyní je čas podívat se na jednodušší způsob skicování této parametrické křivky. Tato metoda využívá skutečnost, že v mnoha, ale ne všech případech můžeme parametr skutečně odstranit z parametrických rovnic a získat funkci zahrnující pouze \(x\) a \(y\). Někdy to nazýváme algebraickou rovnicí, abychom ji odlišili od původních parametrických rovnic., S touto metodou budou dva malé problémy, ale bude snadné tyto problémy řešit. Je však důležité si uvědomit, že to nebudeme vždy schopni udělat.

jak eliminujeme parametr, bude záviset na parametrických rovnicích, které máme. Podívejme se, jak odstranit parametr pro množinu parametrických rovnic, se kterými jsme dosud pracovali.

získání náčrtu parametrické křivky, jakmile odstraníme parametr, se zdá být poměrně jednoduché. Vše, co musíme udělat, je vykreslit rovnici, kterou jsme našli odstraněním parametru., Jak již bylo uvedeno, existují dva malé problémy s touto metodou. První je směr pohybu. Rovnice zahrnující pouze \(x\) a \(y\) nebude dávat směr pohybu parametrické křivky. To je obecně snadný problém opravit však. Podívejme se rychle na deriváty parametrických rovnic z posledního příkladu. Jsou,

\

Všimněte si, že \(x\) derivaci není jako užitečné pro tuto analýzu, jak to bude být jak pozitivní, tak negativní, a tedy \(x\) bude rostoucí a klesající v závislosti na hodnotě \(t\)., To nepomůže se směrem, stejně jako po křivce v obou směrech bude vykazovat jak rostoucí a klesající \(x\).

v některých případech pouze jedna z rovnic, jako je tento příklad, dá směr, zatímco v jiných případech může být použita jedna. Je také možné, že v některých případech by byly k určení směru zapotřebí oba deriváty. Vždy bude záviset na individuální sadě parametrických rovnic.,

druhý problém s odstraněním parametru je nejlépe ilustrován v příkladu, protože na tento problém narazíme ve zbývajících příkladech.

dobře, to byl opravdu dlouhý příklad. Většina těchto typů problémů není tak dlouhá. Právě jsme měli hodně diskutovat v tomto jednom, abychom mohli dostat pár důležitých nápadů z cesty. Zbytek příkladů v této části by neměl trvat tak dlouho, než projde.

nyní se podívejme na další příklad, který ilustruje důležitou představu o parametrických rovnicích.,

takže jsme v posledních dvou příkladech viděli dvě sady parametrických rovnic, které nějakým způsobem daly stejný graf. Přesto, protože oni vysledovat graf jiný počet časů opravdu musíme myslet na ně jako různé parametrické křivky alespoň nějakým způsobem. To se může zdát jako rozdíl, o který se nemusíme starat, ale jak uvidíme v pozdějších sekcích, může to být velmi důležitý rozdíl. V některých pozdějších sekcích budeme potřebovat křivku, která je vysledována přesně jednou.,

než přejdeme k dalším problémům, krátce si uvědomíme, co se stane změnou \(t\) na nt v těchto typech parametrických rovnic. Když máme co do činění s parametrické rovnice zahrnující pouze sines a cosines a oba mají stejný argument, pokud změníme argument z \(t\) na nt jsme jednoduše změnit rychlost, s jakou křivku je dohledat. Pokud \(n > 1\) zvýšíme rychlost a pokud \(n < 1\) snížíme rychlost.

podívejme se na několik dalších příkladů.,

Do tohoto bodu jsme viděli příklady, které by se vysledovat kompletní graf, který máme tím, že odstraní parametr, pokud jsme si dostatečně velkou škálu \(t\). Nicméně, v předchozím příkladu jsme viděli, že to není vždy případ. Je více než možné mít sadu parametrických rovnic, které budou průběžně vysledovat jen část křivky. Obvykle můžeme určit, zda se to stane hledáním limitů na \(x\) a \(y\), které jsou nám uloženy parametrickou rovnicí.,

často použijeme parametrické rovnice k popisu cesty objektu nebo částice. Podívejme se na příklad toho.

v tomto bodě bychom měli dát malé varování. Protože myšlenky se podílejí na ně soustředili jsme se na parametrické křivky, které po částech křivky více než jednou. Nenechte se však příliš zamknout do myšlenky, že se to vždy stane. Mnoho, ne-li většina parametrických křivek bude vysledovat pouze jednou. První, na kterou jsme se podívali, je dobrým příkladem. Tato parametrická křivka nikdy neopakuje žádnou část sebe sama.,

před pokračováním je v této sekci diskutováno jedno konečné téma. Zatím jsme začali s parametrickými rovnicemi a eliminovali parametr pro určení parametrické křivky.

jsou však chvíle, kdy chceme jít opačným směrem. Vzhledem k tomu, funkce nebo rovnice bychom mohli chtít zapsat sadu parametrických rovnic pro něj. V těchto případech říkáme, že parametrizujeme funkci.

pokud vezmeme příklady 4 a 5 jako příklady, můžeme to udělat pro elipsy (a tedy kruhy)., Dané elipsy

\

sada parametrických rovnic pro to by bylo,

\

Tato sada parametrických rovnic bude zjistit, elipsy začíná v bodě \(\left( {a,0} \right)\) a bude sledovat v proti směru hodinových ručiček a bude sledovat přesně jednou v rozsahu \(0 \le t \le 2\pi \). Jedná se o poměrně důležitý soubor parametrických rovnic, jak se používá neustále v některých předmětech se zabývají elipsy a/nebo kruhy.

každá křivka může být parametrizována více než jedním způsobem. Některý z následujících bude také parametrizovat stejnou elipsu.,

\

přítomnost \(\omega \) změní rychlost, kterou se elipsa otáčí, jak jsme viděli v příkladu 5. Všimněte si také, že poslední dva vystopují elipsy ve směru hodinových ručiček (možná to budete chtít ověřit). Také si všimněte, že nebudou všichni začít na stejném místě(pokud si myslíme, že \(t = 0\) jako výchozí bod, který je).

existuje mnoho dalších parametrizací elipsy samozřejmě, ale dostanete nápad. Je důležité si uvědomit, že každá parametrizace jednou vystopuje křivku s potenciálně odlišným rozsahem \(t\)’s., Každá parametrizace se může otáčet různými směry pohybu a může začít v různých bodech.

možná zjistíte, že budete potřebovat parametrizace elipsy, která začíná na určitém místě a má určitý směr pohybu, a tak nyní víte, že se některé práce si můžete napsat sada parametrické rovnice, které vám na chování, které jste po.

nyní si zapište několik dalších důležitých parametrizací a všechny komentáře o směru pohybu, výchozím bodě a rozsahu \(t\) pro jednu stopu (pokud je to možné) jsou stále pravdivé.,

za Prvé, protože kruh není nic jiného než speciální případ elipsy můžeme použít parametrizace elipsy získat parametrické rovnice kružnice střed v počátku o poloměru \(r\). Jeden možný způsob parametrizace kružnice je,

\ \

V tomto okamžiku to nemusí zdát, že všechny užitečné provést parametrizaci funkce, jako je tento, ale existuje mnoho případů, kdy to vlastně bude jednodušší, nebo to dokonce může být požadováno, aby práce s parametrizace místo funkce sám., Bohužel, téměř všechny tyto případy se vyskytují v kurzu kalkulu III.