Zobrazit Mobilní Oznámení, Zobrazit Všechny Poznámky, Skrýt Všechny Poznámky,
sekce 4-11: lineární aproximace
v této části se podíváme na aplikaci ne derivátů, ale na tečnou čáru na funkci. Samozřejmě, abychom získali tečnou čáru, musíme vzít deriváty, takže nějakým způsobem je to také aplikace derivátů.
\
podívejte se na následující graf funkce a její tečnou čáru.
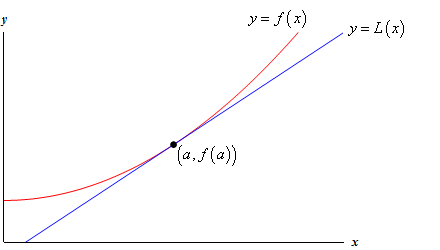
tak proč bychom to dělali? Podívejme se na příklad.,
lineární aproximace dělají velmi dobrou práci při přibližování hodnot \(f\left(x \right)\), pokud zůstaneme „blízko“ \(x = a\). Nicméně, čím dál od \(x = a\) dostaneme horší aproximace je pravděpodobné, že bude. Hlavním problémem je, že jak blízko musíme zůstat na \(x = a\), abychom získali dobrou aproximaci, bude záviset jak na funkci, kterou používáme, tak na hodnotě \(x = a\), kterou používáme. Také často nebude snadný způsob, jak předpovědět, jak daleko od \(x = a\) se můžeme dostat a stále máme „dobrou“ aproximaci.,
podívejme se na další příklad, který se na některých místech skutečně používá poměrně silně.
toto je vlastně poněkud důležitá lineární aproximace. V optice se tato lineární aproximace často používá ke zjednodušení vzorců. Tato lineární aproximace se také používá k popisu pohybu kyvadla a vibrací v řetězci.
















Napsat komentář