muži. Nějak cítím, že se mi líbí to, co říkáš.
Soc. A já, Meno, mám rád to, co říkám.
z Platónova Meno
délka úhlopříčky jednotkového čtverce se rovná odmocnině 2.
délka úhlopříčky čtverce jednotky se rovná √2. No, to není opravdu skvělá zpráva. Každý, kdo někdy narazil na Pythagorovu větu, si je toho vědom., V rovnoramenný pravoúhlý trojúhelník s rameny délky 1, přepona, podle Pythagorovy věty – 12 + 12 = (přepona)2 – je opravdu o délce √2. Motivace pro tuto stránku není ani tak samotná skutečnost, ale způsob, jak ji ukázat bez použití slavné věty. Ve skutečnosti by se dalo tvrdit, že Pythagorova věta mohla být nadužívána, viz zvědavý příklad.
argument, že jde zpátky k obrázku natažený Sokrates v Platónově Meno by bylo známo, že Pythagoras sám, ačkoli žil o století dříve.,
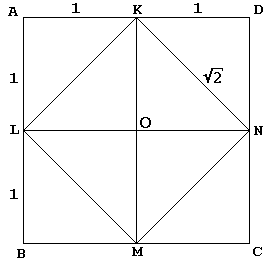
V dialogovém okně, Socrates, v jeho obvyklým způsobem, vede mladý otrok na výstavbu náměstí dvakrát oblasti věnována jedna:
dán čtverec KLMN se středem O je první řez úhlopříčkami na 4 stejné trojúhelníky. Sokrates vkládá KLMN do většího čtvercového ABCD, jako by odrážel tyto trojúhelníky každý ve své hypotenze. Otrok pak přiznává-a kdo by ne? – ten čtvercový ABCD je dvakrát větší než čtvercový KLMN.
po pravdě řečeno, Sokratův čtverec ABCD měřil 4 na straně, takže čtverec KLMN měl plochu 8., Je zřejmé, že když začneme čtvercovým ABCD ze strany 2 (a tedy z oblasti 4), čtvercový KLMN bude mít plochu 2.
nyní je obecně pro kladné číslo a √a definováno jako číslo, jehož čtverec je:
(√a) 2.
na druhou stranu každý student oblastí ví, že plocha čtverce strany b se rovná b2. Z toho pak vyplývá, že strana čtverce s plochou a je přesně √a. došli jsme k závěru, že strana náměstí KLMN se rovná √2. Pro jednoho,
KN = √a.
ústředním bodem argumentu je skutečnost, že v diagramu hraje KN dvojitou roli., Kromě toho, že je jednou ze stran square KLMN, slouží také jako úhlopříčka čtvercového OKDN. Ten je samozřejmě jednotkovým čtvercem, což dokazuje naše tvrzení.
(z trochu jiné perspektivy je stejná epizoda uvedena jinde.)
















Napsat komentář