Dnes se podíváme na nejpopulárnější možnosti cenový model. Model Black Scholes, známý také jako metoda Black-Scholes-Merton, je matematický model pro Smlouvy o cenách. Funguje tak, že odhaduje rozdíly ve finančních nástrojích. Tato technika se opírá o předpoklad, že ceny následují lognormální distribuci. Na základě toho odvozuje hodnotu volby.,

je vhodnější pro možnosti nezávislé na cestě, které investoři nemohou uplatnit před datem splatnosti. Díky tomu se liší od binomického modelu cen opcí, což je metoda neutrální pro hodnocení možností závislých na cestě (např.

analytici a investoři považují Black Scholes za jeden ze základních pojmů moderní finanční teorie.

Zavedena v roce 1973 v Journal of Political Economy, Fischer Black a Myron Scholes, a později postavil na Robert Merton, model získal Nobelovu Cenu za ekonomii v roce 1997.,

model se řídí diferenciální rovnicí, kterou používáme k řešení cen opcí. Používáme standardní variantu modelu pro možnosti evropského stylu. Black Scholes není vhodný pro možnosti amerického stylu, protože nepovažuje investory, kteří mohou tyto možnosti uplatnit kdykoli před datem vypršení platnosti.

metoda předpokládá, že cena podkladové akcie následuje po lognormální distribuci, protože nemůže být záporná. Distribuce, na kterou se model spoléhá, je založena na Brownianově pohybu, teorii předpovídání přirozeně se vyskytujících náhodných jevů.,

použijeme model pro výpočet odhadu ceny opce pomocí následující informace:

  • aktuální cenu;
  • realizační cenu;
  • Čas vypršení platnosti;
  • Očekávaný dividendový výnos;
  • Očekávané úrokové sazby; a
  • Očekávané volatility.

zpočátku model nepovažuje účinek výplaty dividend. Proto se k tomu často přizpůsobuje stanovením hodnoty data ex-dividend podkladového aktiva., Dividendový výnos má za následek snížení aktuální ceny akcií, protože držitel opce se dividend vzdá.

předpoklady

model Black Scholes funguje pouze v případě určitých předpokladů.,s vyskytují během volby životnost (to byl předpoklad v původní model, který analytiků se od té doby odstraněna přidáním dividendový výnos v modelu formule);

  • trhy jsou zcela efektivní, což znamená, že nemůžeme předvídat jejich pohyby;
  • Nákup a prodej možnosti zahrnují žádné transakční náklady;
  • Oba volatilita podkladového aktiva a bezrizikové sazby zůstávají konstantní až do data exspirace, což není správné, protože ve skutečnosti volatility posuny nabídky a poptávky; a
  • výnosy z podkladového aktiva sledovat normální rozdělení.,

    • Black Scholes Vzorec

    model formule je poměrně složitý, matematicky, což není zvláštní problém, jak můžeme využívat specializované nástroje pro výpočet to pro nás. Ale je stále důležité pochopit, jak to funguje.,

    Pro výpočet ceny call opce podle Black Scholes model, můžeme použít následující rovnici:

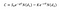
    Kde:

    • S0 je cena akcií;
    • e je exponenciální číslo;
    • q je dividendový výnos procento;
    • T je období (jeden rok bude T=1, zatímco šest měsíců bude T=0.,5);
    • N(d1) je delta opce, což znamená, že změna ve výzvě cena přes posun v cenách akcií;
    • K je realizační cenu;
    • r je bezriziková úroková míra; a
    • N(d2) je pravděpodobnost, že budoucí cena akcie bude vyšší než realizační cena, pravděpodobnost, že budeme používat možnost.

    na Jedné straně je cena akcie vynásobí kumulativního normovaného normálního rozdělení pro d1, a druhá — realizační cena, zlevněné na čase T a pak vynásobí standardní normální kumulativní distribuční d2.,

    Kde můžeme vypočítat d1 a d2 s těmito vzorci:

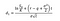
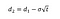
    Kde σ je volatilita výnosů podkladového aktiva.,

    a můžeme použít stejnou logiku pro put opce:

    Připojte se do našeho Newsletter ZDARMA Excel Srovnávací Analýza Šablony

    Příklad Black Scholes Výpočet

    Pro lepší ilustraci pojetí Black Scholes Model, budeme se podívat na následující model. Začínáme s modelovými vstupy., Jak bylo uvedeno výše, potřebujeme následujících šest proměnných pro výpočet hodnoty volání a dát volby.

    Next, budeme počítat možnosti parametrů. Počínaje d1 získáváme 0,39 z našich modelových předpokladů.

    Pro výpočet, můžeme jednoduše převést vzorec pro d1 do aplikace Excel.,

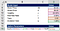
    Following the same approach, we calculate d2, N(d1) and N(d2).

    With those, we can calculate the Call Option Price and the Put Option Price.,

    můžeme použít Volání Dát Parity pravidlo zkontrolujte, zda naše vzorce a výpočty jsou správné.

    Nyní, že máme model pro výpočet Call a Put opce cen, můžeme jít o krok dále a podívejte se na to, jak různé vstupní parametry ovlivnit výsledky našeho modelu., Funkce datové tabulky v Excelu je skvělým nástrojem pro přípravu některých tabulek analýzy citlivosti pro naše proměnné. V našem článku o analýze citlivosti se můžete naučit používat datové tabulky.

    podívejme se na cenu akcií, pokud se změní z €10 na €100 a jak to ovlivní volání a vloží hodnoty. Všimneme si, že možnost volání nemá žádnou hodnotu, dokud cena akcií nedosáhne 40 eur. Vidíme naopak možnost Put, kde jeho hodnota dosáhne nuly, jakmile cena akcií překročí 85 eur.,

    Připravíme-li stejnou citlivost stůl pro Realizační Cenu, můžeme pozorovat opačný vztah. Jak se cena stávky zvyšuje, hodnota hovoru klesá a hodnota Put stoupá.

    Pojďme se také podívat na rizika zdarma, sazba., Jak se zvyšuje, zvyšuje se také požadovaná míra návratnosti. Následně to snižuje hodnotu zásob. Všimneme si přímého vztahu, jak se zvyšuje míra bez rizika, zvyšuje se také hodnota možnosti volání, zatímco hodnota možnosti Put snižuje jeho hodnotu.

    Následující stejný přístup, můžete jít dopředu a podívat se na ostatní parametry a jak ovlivňují Hodnoty Možností., Model aplikace Excel si můžete stáhnout na konci článku a projít tam analýzu citlivosti.

    příklad modelu si můžete stáhnout v Excelu v původním článku.

    závěr

    je důležité si uvědomit, že model Black-Scholes-Merton je teoretický koncept. Využíváme ho k tomu, abychom se pokusili odhadnout chování trhu. Nicméně, když používáme výsledky v našem rozhodovacím procesu, musíme pochopit základní předpoklady v modelu a jak se odchyluje od reality.,

    vzorec pomohl obchodování s opcemi stát se populárnějším, protože to vypadá méně jako hazardní hry. V současné době jsou různé modifikace Black Scholes široce populární jako základní strategie pro kontrolu rizik spojené s volatilitou.

    svou podporu můžete zobrazit sdílením článku s kolegy a přáteli.