Afficher L’avis Mobile afficher toutes les Notes masquer toutes les Notes
Section 3-1 : équations et courbes paramétriques
à ce stade (dans le calcul I et le calcul II), nous avons examiné presque exclusivement les fonctions sous la forme \(y = f\left( x \right)\) OU \(x = h\left( y \right)\) et presque toutes les formules que nous avons développées exigent que les fonctions soient sous l’une de ces deux formes. Le problème est que toutes les courbes ou équations que nous aimerions examiner ne tombent pas facilement sous cette forme.
Prenez, par exemple, un cercle. Il est assez facile d’écrire l’équation d’un cercle centré à l’origine et de rayon \(r\).,
\
Cependant, nous ne pourrons jamais écrire l’équation d’un cercle comme une seule équation dans l’une ou l’autre des formes ci-dessus. Bien sûr, nous pouvons résoudre pour \(x\) ou \(y\) comme le montrent les deux formules suivantes
\
mais il y a en fait deux fonctions dans chacune d’entre elles. Chaque formule donne une partie du cercle.
\
Malheureusement, nous travaillons sur l’ensemble du cercle, ou tout simplement ne peut pas dire que nous allons travailler sur une seule partie. Même si nous pouvons réduire les choses à une seule de ces parties, la fonction est encore souvent assez désagréable à travailler.,
\
Cette troisième variable est généralement notée \(t\) (comme nous l’avons fait ici), mais ne doit pas être bien sûr. Parfois, nous limiterons les valeurs de \(t\) que nous utiliserons et à d’autres moments nous ne le ferons pas. cela dépendra souvent du problème et de ce que nous essayons de faire.
pour vous aider à visualiser ce qu’est une courbe paramétrique, imaginez que nous avons un grand réservoir d’eau en mouvement constant et que nous déposons une balle de ping-pong dans le réservoir., Le point \(\left( {x,y} \right) = \left( {f\left( t \right),g\left( t \right)} \right)\) représentera alors l’emplacement de la balle de ping pong dans le réservoir au moment \(t\) et la courbe paramétrique sera une trace de tous les endroits de la balle de ping-pong. Notez que ce n’est pas toujours une analogie correcte, mais il est utile au départ pour aider à visualiser exactement ce qu’est une courbe paramétrique.
l’Esquisse d’une courbe paramétrique n’est pas toujours une chose facile à faire. Jetons un coup d’œil à un exemple pour voir une façon d’esquisser une courbe paramétrique., Cet exemple illustrera également pourquoi cette méthode n’est généralement pas la meilleure.
à ce stade, notre seule option pour dessiner une courbe paramétrique est de choisir les valeurs de \(T\), de les brancher dans les équations paramétriques, puis de tracer les points. Alors, branchons quelques \(t\).,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Malheureusement, il n’y a pas de vraie réponse à cette question à ce stade. Nous choisissons simplement \(t\) jusqu’à ce que nous soyons assez confiants que nous avons une bonne idée de ce à quoi ressemble la courbe. C’est ce problème avec la sélection de « bonnes” valeurs de \(t\) qui fait de cette méthode d’esquisse de courbes paramétriques l’un des choix les plus pauvres. Parfois, nous n’avons pas le choix, mais si nous avons un choix que l’on doit l’éviter.
nous discuterons d’une autre méthode graphique dans des exemples ultérieurs qui aideront à expliquer comment ces valeurs de \(t\) ont été choisies.,
nous avons encore une idée à discuter avant d’esquisser la courbe. Les courbes paramétriques ont une direction de mouvement. La direction du mouvement est donnée en augmentant \(t\). Ainsi, lorsque vous tracez des courbes paramétriques, nous incluons également des flèches qui montrent la direction du mouvement. Nous allons souvent donner la valeur de \(t\) qui a donné des points spécifiques sur le graphique ainsi de préciser la valeur de \(t\) qui a donné ce point particulier.
Voici l’esquisse de cette courbe paramétrique.
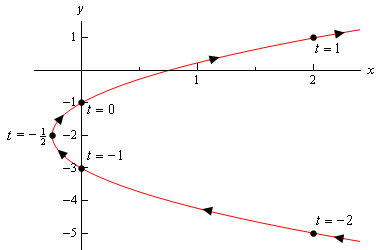
Donc, il semble que nous avons une parabole qui s’ouvre vers la droite.,
avant de terminer cet exemple, il y a un point quelque peu important et subtil que nous devons d’abord discuter. Notez que nous avons fait en sorte d’inclure une partie de l’esquisse à la droite des points correspondant à \(t = 2\) et \(t = 1\) pour indiquer qu’il y a des parties de l’esquisse là. Si nous avions simplement arrêté l’esquisse à ces points, nous indiquons qu’il n’y avait pas de partie de la courbe à droite de ces points et qu’il y en aura clairement. Nous n’avons juste calculé aucun de ces points.,
cela peut sembler un point sans importance, mais comme nous le verrons dans l’exemple suivant, il est plus important que nous ne le pensons.
avant d’aborder un moyen beaucoup plus simple d’esquisser ce graphique, abordons d’abord la question des limites du paramètre. Dans l’exemple précédent, nous n’avions aucune limite sur le paramètre. Sans limites sur le paramètre, le graphique continuera dans les deux sens comme indiqué dans l’esquisse ci-dessus.
nous aurons souvent des limites sur le paramètre cependant et cela affectera l’esquisse des équations paramétriques., Pour voir cet effet, regardons une légère variation de l’exemple précédent.
notez que la seule différence ici est la présence des limites sur\(t\). Toutes ces limites nous disent que nous ne pouvons prendre aucune valeur de \(t\) en dehors de cette plage. Par conséquent, la courbe paramétrique ne sera qu’une partie de la courbe ci-dessus. Voici la courbe paramétrique pour cet exemple.,
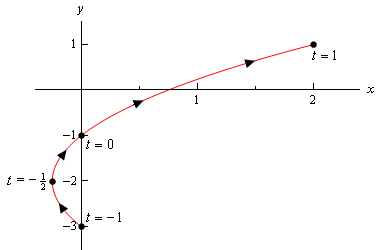
notez qu’avec cette esquisse, nous avons commencé et arrêté l’esquisse directement sur les points provenant des points de fin de la plage de \(t\). contrastez avec l’esquisse de l’exemple précédent où nous avions une partie de l’esquisse à droite des points « Début” et « fin” que nous avons calculés.
dans ce cas, la courbe commence à \(t = – 1\) et se termine à \(t = 1\), alors que dans l’exemple précédent, la courbe ne commençait pas vraiment aux points les plus à droite que nous avons calculés., Nous devons être clairs dans nos croquis si la courbe commence / se termine juste à un point, ou si ce point était simplement le premier/dernier que nous avons calculé.
Il est maintenant temps de jeter un oeil à une méthode plus facile de réaliser un croquis de cette courbe paramétrique. Cette méthode utilise le fait que dans de nombreux cas, mais pas tous, nous pouvons réellement éliminer le paramètre des équations paramétriques et obtenir une fonction impliquant uniquement \(x\) et \(y\). Nous appellerons parfois cela l’équation algébrique pour la différencier des équations paramétriques d’origine., Il y aura deux petits problèmes avec cette méthode, mais il sera facile de résoudre ces problèmes. Il est important de noter cependant que nous ne serons pas toujours en mesure de le faire.
la façon dont nous éliminons le paramètre dépendra des équations paramétriques que nous avons. Voyons comment éliminer le paramètre pour l’ensemble des équations paramétriques avec lesquelles nous avons travaillé jusqu’à présent.
obtenir une esquisse de la courbe paramétrique une fois que nous avons éliminé le paramètre semble assez simple. Tout ce que nous devons faire est de représenter graphiquement l’équation que nous avons trouvée en éliminant le paramètre., Comme indiqué précédemment cependant, il y a deux petits problèmes avec cette méthode. Le premier est la direction du mouvement. L’équation impliquant seulement \(x\) et \(y\) ne donnera pas la direction de mouvement de la courbe paramétrique. C’est généralement un problème facile à résoudre, cependant. Jetons un coup d’œil rapide aux dérivées des équations paramétriques du dernier exemple. Ils sont,
\
notez que la dérivée \(x\) n’est pas aussi utile pour cette analyse car elle sera à la fois positive et négative et donc \(x\) augmentera et diminuera en fonction de la valeur de \(t\)., Cela n’aide pas beaucoup avec la direction car suivre la courbe dans les deux sens montrera à la fois croissant et décroissant \(x\).
dans certains cas, une seule des équations, comme cet exemple, donnera la direction alors que dans d’autres cas, l’une ou l’autre pourrait être utilisée. Il est également possible que, dans certains cas, les deux dérivés soient nécessaires pour déterminer la direction. Il sera toujours dépendant de l’ensemble individuel des équations paramétriques.,
le deuxième problème avec l’élimination du paramètre est mieux illustré dans un exemple car nous rencontrerons ce problème dans les exemples restants.
D’accord, c’était un très long exemple. La plupart de ces types de problèmes ne sont pas aussi longs. Nous avions juste beaucoup à discuter dans celui-ci afin que nous puissions obtenir quelques idées importantes de la route. Le reste des exemples dans cette section ne devrait pas prendre autant de temps à passer.
maintenant, regardons un autre exemple qui illustrera une idée importante sur les équations paramétriques.,
Donc, nous l’avons vu dans les deux derniers exemples, deux ensembles d’équations paramétriques, en quelque sorte, a donné le même graphique. Pourtant, parce qu’ils ont tracé le graphique un nombre différent de fois, nous devons vraiment les considérer comme des courbes paramétriques différentes, au moins d’une manière ou d’une autre. Cela peut sembler une différence dont nous n’avons pas à nous soucier, mais comme nous le verrons dans les sections ultérieures, cela peut être une différence très importante. Dans certaines sections suivantes nous allons avoir besoin d’une courbe est tracée exactement une fois.,
avant de passer à d’autres problèmes, reconnaissons brièvement ce qui se passe en changeant le \(t\) en nt dans ces types d’équations paramétriques. Lorsque nous traitons des équations paramétriques impliquant uniquement des sinus et des cosinus et qu’ils ont tous deux le même argument si nous changeons l’argument de \(t\) à nt, nous changeons simplement la vitesse avec laquelle la courbe est tracée. Si \(n > 1\), nous allons augmenter la vitesse et si \(n < 1\) va diminuer la vitesse.
jetons un coup d’œil à quelques autres exemples.,
à ce stade, nous avons vu des exemples qui retraceraient le graphique complet que nous avons obtenu en éliminant le paramètre si nous prenions une plage suffisamment grande de \(T\). cependant, dans l’exemple précédent, nous avons maintenant vu que ce ne sera pas toujours le cas. Il est plus que possible d’avoir un ensemble d’équations paramétriques qui ne traceront en permanence qu’une partie de la courbe. Nous pouvons généralement déterminer si cela se produira en recherchant des limites sur \(x\) et \(y\) qui nous sont imposées par l’équation paramétrique.,
Nous utiliserons souvent des équations paramétriques pour décrire le chemin d’un objet ou d’une particule. Prenons un oeil à un exemple.
nous devrions donner un petit avertissement à ce stade. En raison des idées qui y sont impliquées, nous nous sommes concentrés sur les courbes paramétriques qui ont retracé des parties de la courbe plus d’une fois. Cependant, ne vous laissez pas trop enfermer dans l’idée que cela se produira toujours. Beaucoup, sinon la plupart des courbes paramétriques ne seront tracées qu’une seule fois. Le premier que nous avons examiné en est un bon exemple. Cette courbe paramétrique ne répétera jamais aucune partie d’elle-même.,
Il y a un dernier thème abordé dans cette section avant de passer. Jusqu’à présent, nous avons commencé avec des équations paramétriques et éliminé le paramètre pour déterminer la courbe paramétrique.
Cependant, il ya des moments où nous voulons aller dans l’autre sens. Étant donné une fonction ou d’une équation on peut vouloir écrire un ensemble d’équations paramétriques pour elle. Dans ces cas, nous disons que nous paramétrons la fonction.
Si nous prenons les exemples 4 et 5 comme exemples, nous pouvons le faire pour les ellipses (et donc les cercles)., Compte tenu de l’ellipse
\
un ensemble d’équations paramétriques pour il serait,
\
Cet ensemble d’équations paramétriques trace l’ellipse du point \(\left( {a,0} \right)\) et trace dans le sens anti-horaire et trace exactement une fois dans l’intervalle \(0 \le t \le 2\pi \). Il s’agit d’un ensemble assez important d’équations paramétriques car il est utilisé continuellement dans certains sujets traitant des ellipses et/ou des cercles.
chaque courbe peut être paramétrée de plusieurs façons. L’un des éléments suivants paramétrera également la même ellipse.,
\
La présence du \(\omega \) va changer la vitesse de l’ellipse tourne comme nous l’avons vu dans l’Exemple 5. Notez également que les deux derniers traceront des ellipses dans le sens des aiguilles d’une montre (vous voudrez peut-être vérifier cela). Notez également qu’ils ne commenceront pas tous au même endroit (si nous pensons à \(t = 0\) comme point de départ).
Il y a bien sûr beaucoup plus de paramétrisations d’une ellipse, mais vous avez l’idée. Il est important de se rappeler que chaque paramétrage tracera la courbe une fois avec une plage potentiellement différente de \(t\)’s., Chaque paramétrage peut tourner avec différentes directions de mouvement et peut commencer à différents points.
Vous pouvez trouver que vous avez besoin d’un paramétrage d’une ellipse qui commence à un endroit particulier et a un sens du mouvement et donc, vous savez maintenant qu’avec un peu de travail, vous pouvez écrire un ensemble d’équations paramétriques qui vous donnera le comportement que vous êtes après.
maintenant, écrivons quelques autres paramétrisations importantes et tous les commentaires sur la direction du mouvement, le point de départ et la plage de \(T\) pour une trace (le cas échéant) sont toujours vrais.,
tout d’Abord, parce qu’un cercle n’est rien de plus qu’un cas particulier d’une ellipse, on peut utiliser le paramétrage d’une ellipse pour obtenir les équations paramétriques d’un cercle centré à l’origine de rayon \(r\) ainsi. Une façon possible de paramétrer un cercle est,
\ \
à ce stade, il peut ne pas sembler très utile de faire un paramétrage d’une fonction comme celle-ci, mais il y a beaucoup de cas où il sera plus facile, ou il peut même être nécessaire, de travailler avec le paramétrage au lieu de la fonction elle-même., Malheureusement, presque tous ces cas se produisent dans un cours de calcul III.
















Laisser un commentaire