Calcul I-Approximations linéaires

Afficher L’avis Mobile afficher toutes les Notes masquer toutes les Notes

Section 4-11 : Approximations linéaires

dans cette section, nous allons examiner une application non pas de dérivées mais de la ligne tangente à une fonction. Bien sûr, pour obtenir la ligne tangente, nous devons prendre des dérivées, donc d’une certaine manière, c’est aussi une application de dérivées.

\

regardez le graphique suivant d’une fonction et de sa ligne tangente.

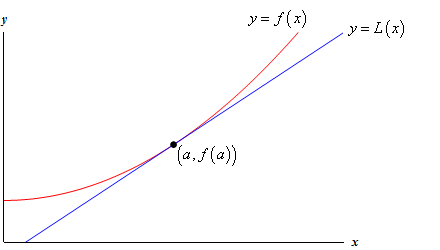
Alors, pourquoi devrions-nous le faire? Prenons un oeil à un exemple.,

les approximations linéaires font un très bon travail d’approximation des valeurs de \(f\left( x \right)\) tant que nous restons « proches” de \(x = a\). Cependant, plus nous nous éloignons de \(x = a\), plus l’approximation est susceptible d’être mauvaise. Le principal problème ici est que la proximité avec laquelle nous devons rester à \(x = a\) pour obtenir une bonne approximation dépendra à la fois de la fonction que nous utilisons et de la valeur de \(x = a\) que nous utilisons. En outre, il n’y aura souvent pas de moyen facile de prédire à quelle distance de \(x = a\) Nous pouvons obtenir et avoir toujours une « bonne” approximation.,

jetons un coup d’œil à un autre exemple qui est en fait assez utilisé à certains endroits.

il s’agit en fait d’une approximation linéaire quelque peu importante. En optique, cette approximation linéaire est souvent utilisée pour simplifier les formules. Cette approximation linéaire est également utilisée pour aider à décrire le mouvement d’un pendule et les vibrations dans une corde.