Les vecteurs sont largement utiles en science pour décrire tout ce qui a à la fois une direction et une magnitude. Ils sont généralement dessinés à l’aide de flèches pointues, dont la longueur représentera la magnitude du vecteur. La passe d’un quart-arrière est l’exemple simple car elle a la direction généralement quelque part en bas du terrain et une magnitude. Parfois, nous devons gérer deux vecteurs ensemble travaillant sur un objet. Dans de tels cas, les angles entre ces vecteurs sont importants., Ce sujet expliquera l’angle entre deux vecteurs formule ainsi que des exemples. Laissez-nous apprendre!
Notion de Vecteurs
en dehors du terrain, les vecteurs peuvent être utilisés pour représenter n’importe quel nombre d’objets physiques ou des activités. Exemple. Le vent, par exemple, est une quantité vectorielle. C’est parce qu’à n’importe quel endroit donné, il a une direction ainsi que la magnitude. Nous pouvons alors faire une carte du flux d’air à tout moment en dessinant les vecteurs du vent pour un certain nombre de lieux géographiques différents.
de nombreuses propriétés des objets en mouvement sont également des sortes de vecteurs., En boule de billard, son vecteur vitesse décrit son mouvement. Il montre la direction des marques de flèche vectorielles comme la direction du mouvement, et la longueur du vecteur représente la vitesse de la balle.
l’élan de la boule de billard est également un exemple de grandeur vectorielle. Comme il est égal à la masse fois la vitesse. Par conséquent, le vecteur momentum des billes pointe dans la même direction que son vecteur vitesse. Et la magnitude du vecteur d’élan sera le produit de multiplication de la vitesse de la balle et de sa masse.,
en termes de mathématiques, un vecteur est tout objet qui a une grandeur et une direction définissables. Comme les vecteurs ne sont pas les mêmes que les lignes ou les formes standard, Nous devons utiliser des formules spéciales pour trouver des angles entre eux.
La Formule de l’Angle entre Deux Vecteurs
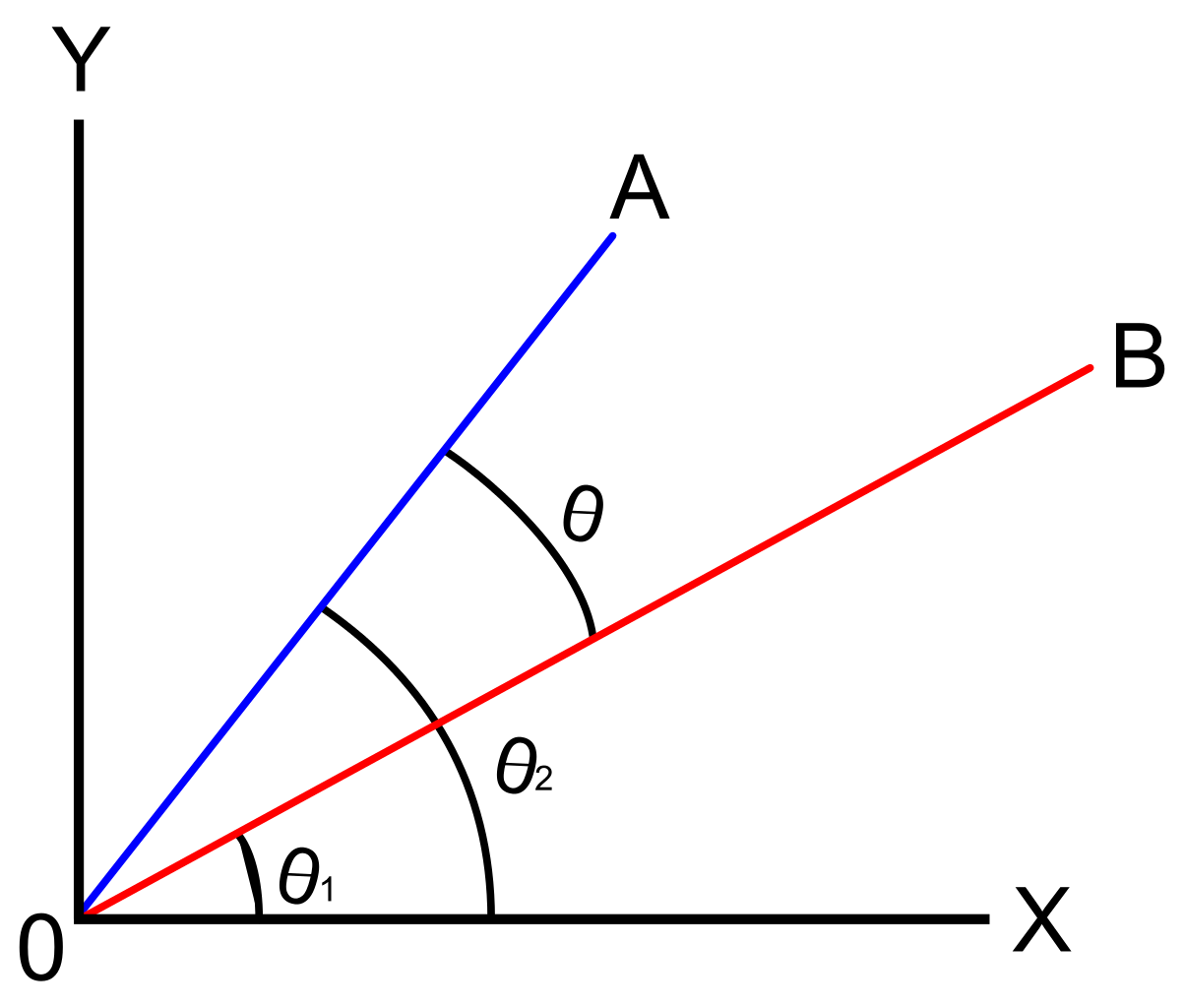
L’angle entre deux vecteurs seront reportés par un seul point, qui est appelé le plus court de l’angle à laquelle nous devons nous tourner autour de l’un des vecteurs de la position de co-directionnel avec un autre vecteur.,
la discussion sur les angles de direction des vecteurs se concentre sur la recherche de l’angle d’un vecteur par rapport à l’axe X positif. Cela se concentrera sur l’angle entre deux vecteurs dans la position standard. Un vecteur est dit en position standard si le premier point est l’origine (0, 0).
Si les deux vecteurs sont supposés a et b, alors le point créé est défini comme A.B. supposons que ces deux vecteurs sont séparés par angle \(\thêta\). Pour savoir quelle est la mesure d’angle, Nous allons résoudre à l’aide de la formule donnée:
nous connaissons le produit dot:
\(\vec{a}.,\vec{b} =|\vec{a}||\vec{b}|cos\theta\)
Maintenant, l’angle entre deux vecteurs, la formule est:
\(\theta = cos^{-1}\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}\)
Où \\(theta\) est l’angle entre a et b des vecteurs.
Exemples Résolus pour l’Angle entre Deux Vecteurs Formule
Q. 1: Calculer l’angle entre deux vecteurs 3i + 4j – k et 2i – j + k.
la Solution: Laisser,
a = 3i + 4j – k et
b = 2i – j + k
On définit le produit scalaire:
un .b = (3i + 4j-k–.(2i-j + k)
















Laisser un commentaire