racines d’un polynôme

une racine ou zéro d’une fonction est un nombre qui, lorsqu’il est branché pour la variable, rend la fonction égale à zéro. Ainsi, les racines D’un polynôme P (x) sont des valeurs de x telles que P(x) = 0.

le théorème des zéros rationnels

Le théorème des zéros rationnels déclare:

Nous pouvons utiliser le théorème des zéros rationnels pour trouver tous les zéros rationnels d’un polynôme., Voici les étapes:

  1. Organiser le polynôme dans l’ordre décroissant
  2. Écrire tous les facteurs de la constante de terme. Ce sont toutes les valeurs possibles de P.
  3. Notez tous les facteurs du coefficient principal. Ce sont toutes les valeurs possibles de q.
  4. Écrivez toutes les valeurs possibles de . Rappelez-vous que, depuis les facteurs peuvent être négatifs, et doivent être inclus. Simplifiez chaque valeur et rayez les doublons.,
  5. Utiliser synthétique de la division pour déterminer les valeurs de pour lequel P() = 0. Ce sont toutes les racines rationnelles de P(x).

exemple: trouver tous les zéros rationnels de P(x) = x3-9x + 9 + 2×4-19×2.

Figure %: Synthétique Division

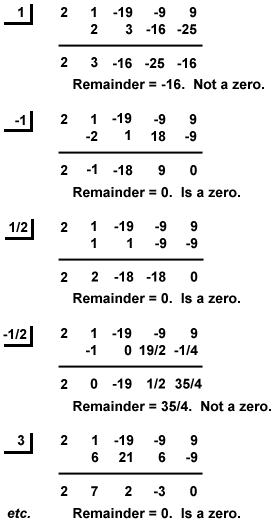
Ainsi, le rationnel racines de P(x) x = – 3, -1, 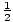, et 3.

on peut souvent utiliser le théorème des zéros rationnels pour factoriser un polynôme., En utilisant la division synthétique, nous pouvons trouver une racine réelle a et nous pouvons trouver le quotient lorsque P (x) est divisé par x – A. Ensuite, nous pouvons utiliser la division synthétique pour trouver un facteur du quotient. Nous pouvons continuer ce processus jusqu’à ce que le polynôme ait été complètement factorisé.