Quando os ângulos de um triângulo não se somam a 180 graus

1. Introdução os ângulos de um triângulo somam-se a 180 graus ou a $\pi$ radians? A resposta é “às vezes sim, às vezes não”. É uma pergunta importante? Sim, porque leva a um entendimento de que existem geometrias diferentes baseadas em axiomas diferentes ou “regras do jogo da geometria”. É uma pergunta significativa? Bem, não, pelo menos não até Termos concordado com o significado das palavras “ângulo” e “triângulo”, não até conhecermos as regras do jogo., Neste artigo, vamos discutir brevemente subjacente axiomas e dar uma simples prova de que a soma dos ângulos de um triângulo na superfície de uma esfera unitária não é igual a $\pi$, mas como $\pi$, mais a área do triângulo. Usaremos o fato de que a área da superfície de uma esfera unitária é de US $4\pi$.2. O grande Teorema

Antes de podermos dizer o que é um triângulo precisamos concordar no que queremos dizer com pontos e linhas. Estamos trabalhando na geometria esférica (literalmente geometria na superfície de uma esfera)., Nesta geometria, o espaço é a superfície da esfera; os pontos são pontos nessa superfície, e a linha de menor distância entre dois pontos é o grande círculo contendo os dois pontos. Um grande círculo (como o Equador) corta a esfera em dois hemisférios iguais. Esta geometria tem aplicações óbvias para distâncias entre lugares e rotas aéreas na Terra.,

girar a esfera, mostrando grande círculo

O ângulo entre dois grandes círculos em um ponto P é a Euclidiana ângulo entre as direções dos círculos (ou estritamente entre tangentes aos círculos P). Isto não apresenta nenhuma dificuldade na navegação na terra porque em qualquer ponto pensamos no ângulo entre duas direções como se a Terra fosse plana naquele ponto.uma lune é uma parte da superfície da esfera delimitada por dois grandes círculos que se encontram em pontos antipodais., Primeiro consideramos a área de uma lune e, em seguida, introduzimos outro grande círculo que divide a lune em triângulos.

girar a esfera mostrando 4 lunes

Lema.

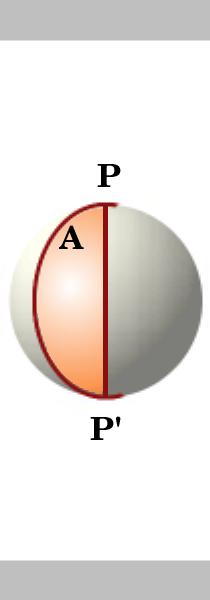
a área de uma lune num círculo de raio unitário é duas vezes o seu ângulo, ou seja, se o ângulo da lune for a, então a sua área é 2A. dois grandes círculos que se cruzam nos pontos antipodais P E P’ dividem a esfera em 4 lunes. A área da superfície de uma esfera unitária é de $ 4\pi$.,

As áreas dos lunes são proporcionais aos seus ângulos em P de modo que a área de uma lune com ângulo A é

${\frac{a}{2\pi}\times {4\pi}= {2A}}$

Exercício 1.quais são as áreas dos outros 3 lunes? As suas quatro áreas somam $ 4\pi$?verifique aqui as suas respostas .

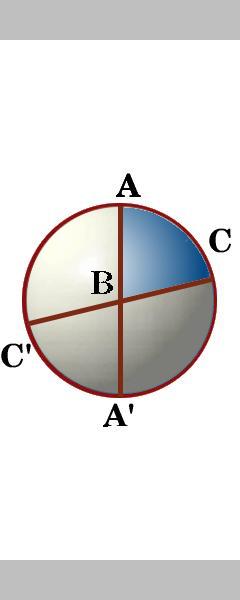
os lados de um triângulo ABC são segmentos de três grandes círculos que realmente cortam a superfície da esfera em oito triângulos esféricos. Entre os dois grandes círculos através do ponto A Há quatro ângulos., Nós rótulo o ângulo dentro do triângulo ABC como Um ângulo, e da mesma forma, os outros ângulos do triângulo ABC como ângulo B e o ângulo C.

girar a esfera, mostrando 8 triângulos

Exercício 2

Girar a esfera a oito triângulos e dizer se algum deles tem a mesma área? Veja aqui as suas respostas .

Teorema.

considere um triângulo esférico ABC na esfera unitária com ângulos A, B E C. Então a área do triângulo ABC é

A + B + C – $\pi$.,

O diagrama mostra uma vista olhando para baixo no hemisfério que tem a linha através de AC como seu limite. As regiões marcadas Área 1 e área 3 são lunes com ângulos A E C, respectivamente. Considere os lunes através de B E B’. O triângulo ABC é congruente ao Triângulo A’ B’, de modo que a área sombreada em forma de laço, marcada Área 2, que é a soma das áreas dos triângulos ABC e a’BC’, é igual à área da lune com ângulo B, que é igual a 2B.,

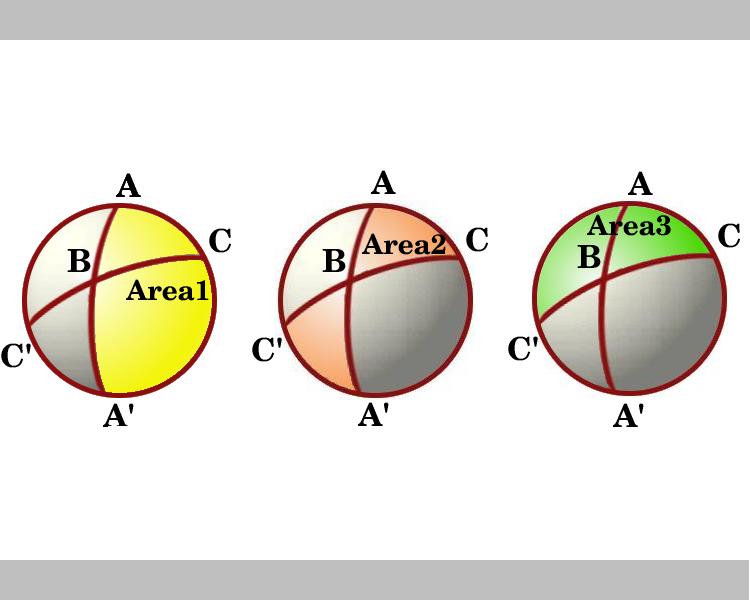
Então, no diagrama vemos as áreas de três segundas-feiras e, usando o lema, estes são:

Área 1 = 2A
Área 2 = 2B
Área 3 = 2C

No somando estes três áreas que incluem a área do triângulo ABC, três vezes., Hence

3., Geometria não-euclidiana às vezes descobertas revolucionárias não são nada mais do que ver o que tem estado debaixo dos nossos narizes o tempo todo. Este foi o caso da descoberta da geometria não euclidiana no século XIX. Para cerca de 2000 anos depois de Euclides escreveu os seus “Elementos”, em 325 A.C., as pessoas tentaram provar o postulado paralelo como um teorema em geometria a partir dos outros axiomas, mas sempre falhou e thatis uma longa história., Enquanto isso, os matemáticos estavam usando geometria esférica o tempo todo, uma geometria que obedece a outros axiomas da Geometria Euclidiana e contém muitos dos mesmos teoremas, mas em que o paralelo postulado não espera. Sempre tiveram um exemplo de geometria não euclidiana debaixo de seus narizes.

pense numa linha L e num ponto P não em L. A grande questão é: “quantas linhas podem ser traçadas através de P paralelas a L? Na geometria euclidiana a resposta é `exatamente uma ” e esta é uma versão do postulado paralelo., Se a soma dos ângulos de cada triângulo na geometria é $\pi$ radians então o postulado paralelo mantém e vice-versa, as duas propriedades são equivalentes.

Na geometria esférica, os axiomas básicos que assumimos (regras do jogo) são diferentes da Geometria Euclidiana – esta é uma Geometria Não-Euclidiana. Vimos que na geometria esférica os ângulos dos triângulos nem sempre somam até $\pi$ radians para que não esperássemos que o postulado paralelo se mantivesse., Na geometria esférica, as linhas rectas (linhas de menor distância ou geodésicas)são grandes círculos e cada linha na geometria corta cada outra linha em dois pontos. A resposta para a grande questão sobre paralelos é: “se temos uma linha L e um ponto P não em L, então não há linhas através de P paralelas à linha L.,”

Os matemáticos gregos (por exemplo, Ptolomeu c 150) calculada com as medições do ângulo direito triângulos esféricos e trabalhou com fórmulas de trigonometria esférica e Árabe matemáticos (por exemplo Jabir ibn Aflah c 1125 e Nasir ed-din c 1250) estendeu o trabalho ainda mais. A fórmula discutida neste artigo foi descoberta por Harriot em 1603 e publicada por Girard em 1629. Outras medidas do assunto foram desenvolvidas por Saccerhi (1667 – 1733).,

tudo isso foi em grande parte não notado pelos descobridores do século XIX da geometria hiperbólica, que é outra geometria não euclidiana onde o postulado paralelo não se mantém. Na geometria esférica (também chamada de geometria elíptica) os ângulos dos triângulos somam mais de $\pi$ radians e na geometria hiperbólica os ângulos dos triângulos somam até menos de $\pi$ radians.

para mais leitura Veja o artigo de Alan Beardon ‘ quantas geometrias existem?”and the article by Keith Carne “Strange Geometries”., Existem algumas atividades práticas que você pode tentar por si mesmo para explorar essas geometrias mais longe a ser encontrado em