Um vetor tem magnitude (quanto tempo) e direção:
Aqui estão dois vetores:

o Que pode ser multiplicado usando o “Produto escalar” (ver também Cruz do Produto).,
podemos calcular o Produto escalar de dois vetores desta forma:

a · b = |a| x |b| x cos(θ)
em que:
|a| é a dimensão (comprimento) de um vetor
|b| é a dimensão (comprimento) do vetor b
θ é o ângulo entre a e b
Então, nós multiplique o comprimento de uma vezes o comprimento de b, então multiplique pelo co-seno do ângulo entre a e b
OU podemos calculá-lo desta forma:
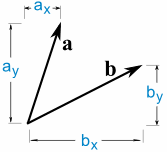
a · b = ax × bx + ay × por
Então, multiplicando o x, multiplicar o y, em seguida, adicionar.,
ambos os métodos funcionam!
E o resultado é um número (chamado de “escalar” para que saibamos que não é um vetor). nota: pode usar o cálculo vectorial para o ajudar.
Why cos(θ) ?
OK, para multiplicar dois vectores faz sentido multiplicar os seus comprimentos juntos, mas apenas quando apontam na mesma direcção.,
Assim, podemos fazer um “ponto de, na mesma direção” como os outros, multiplicando-os por cos(θ):
 |
 |
|
| Tomamos o componente de um que se encontra ao lado de b |
brilhando Como uma luz para ver onde a sombra fica |
em SEGUIDA, multiplicamos !,
ângulos rectos
quando dois vectores estão em ângulos rectos um para o outro, o produto dos pontos é zero.
esta pode ser uma maneira útil de descobrir se dois vetores estão em ângulos retos.
três ou mais dimensões
tudo isto funciona bem em 3 (ou mais) dimensões, também.
e pode ser realmente muito útil!
tentei um cálculo como esse uma vez, mas trabalhei todos em ângulos e distâncias … era muito difícil, envolvia muita trigonometria e doía-me o cérebro. O método acima é muito mais fácil.,
produto cruzado
o produto Ponto dá uma resposta escalar (número comum), e às vezes é chamado de produto escalar.
mas há também o produto cruzado que dá um vetor como uma resposta, e é às vezes chamado de produto vetorial.

















Deixe uma resposta