Homens. Sinto, de alguma forma, que gosto do que estás a dizer.
Soc. E eu, Meno, gosto do que estou a dizer.
do Meno de Platão
o comprimento da diagonal do quadrado da unidade é igual à raiz quadrada de 2.
O comprimento da diagonal do quadrado unitário é igual a √2. Bem, isto não são boas notícias. Todo aquele que já se deparou com o teorema de Pitágoras está ciente do fato., No triângulo de isósceles com as pernas de comprimento 1, a hipotenusa, de acordo com o teorema de Pitágoras – 12 + 12 = (hipotenusa)2 – é de fato de comprimento √2. A motivação para esta página não é tanto esse fato em si, mas a maneira de mostrá-lo sem um recurso ao famoso Teorema. De fato, pode-se argumentar que o teorema de Pitágoras pode ter sido super utilizado, veja um exemplo curioso.um argumento que remonta à figura desenhada por Sócrates no Meno de Platão pode ter sido conhecido pelo próprio Pitágoras, embora este último tenha vivido um século antes.,
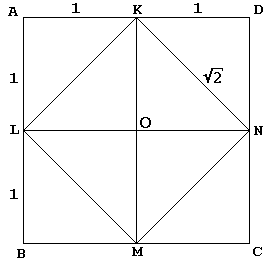
na janela, Sócrates, à sua maneira habitual, leva um jovem escravo a uma construção de um quadrado duas vezes a área do dado:
O dado KLMN quadrado com centro O é primeiro cortado pelas suas diagonais em 4 triângulos iguais. Sócrates incorpora KLMN em um ABCD quadrado maior como se refletindo estes triângulos cada um em sua hipotenusa. O escravo então admite – e quem não o faria? – o quadrado ABCD é duas vezes maior que o quadrado KLMN.
verdade seja dita, o quadrado ABCD de Sócrates medido 4 no lado, tal que o quadrado KLMN tinha área de 8., É claro que quando começamos com o quadrado ABCD do lado 2 (e, portanto, da área 4), o quadrado KLMN terá área de 2.
agora, em geral, para um número positivo A, √A é definido como um número cujo quadrado é A:
(√a)2.
Por outro lado, todo estudante de áreas sabe, que a área de um quadrado do lado b é igual a b2. Segue-se então que o lado de um quadrado com área a é exatamente √a. concluímos que o lado do quadrado KLMN é igual a √2. Para um,
kn = √a.
o ponto central do argumento é o fato de que, no diagrama, KN desempenha um papel duplo., Além de ser um dos lados da KLMN quadrada, também serve como uma diagonal da OKDN quadrada. Este último é, evidentemente, um quadrado unitário, o que prova a nossa afirmação.
(de uma perspectiva um pouco diferente, o mesmo episódio é mencionado em outros lugares.)
















Deixe uma resposta