Partilhar no

Conteúdo (Clique para pular para a seção):

  1. Tudo sobre o…
    • Médio
    • Mode
    • Mediana
  2. Como encontrar a média, moda e mediana com a mão.
  3. Encontrar a média, moda e mediana com Tecnologia de:
    • SPSS
    • TI83

Descrição

Preso sobre como encontrar a média, mediana, & modo de estatísticas?,

  1. A média é a média de um conjunto de dados.
  2. o modo é o número mais comum em um conjunto de dados.
  3. a mediana é o meio do conjunto de números.

das três, a média é a única que requer uma fórmula. Eu gosto de pensar nisso no outro sentido do dicionário da palavra (como em, é MAU em oposição a nice!). Isso é porque, comparado com os outros dois, não é tão fácil trabalhar com eles.,


Dicas para lembrar a diferença

com dificuldade de lembrar a diferença entre a média, moda e mediana? Aqui estão algumas dicas que podem ajudar. Você também pode verificar os tutores em Chegg.com (os seus primeiros 30 minutos são grátis!).

  • “A La mode” é uma palavra francesa que significa moda ; também se refere a uma maneira popular de servir sorvete. Então “Mode” é o membro mais popular ou na moda de um conjunto de números. O modo palavra também é como a maioria.,
  • A ” média “requer que você faça aritmética (adicionando todos os números e dividindo) de modo que essa seja a” média”.
  • “mediana “tem o mesmo número de letras que”Médio”.

ainda não têm a certeza de qual é a diferença entre os três? Assista ao vídeo ou Leia para obter mais informações:

por favor aceite estatísticas, cookies de marketing para assistir a este vídeo.

a média

média vs. mediana
média vs., Média
Específico “Significa” comumente utilizado em Stats
Outros Tipos

Significa vs Mediana

Ambos são medidas de onde o centro de um conjunto de dados se encontra (chamado de “Tendência Central” nas estatísticas), mas eles geralmente são de números diferentes. Por exemplo, tome esta lista de números: 10, 10, 20, 40, 70.

  • médio (informalmente, a “média”) é encontrada adicionando todos os números juntos e dividindo pelo número de itens no conjunto: 10 + 10 + 20 + 40 + 70 / 5 = 30.
  • a mediana é encontrada ordenando o conjunto do mais baixo para o mais alto e encontrando o meio exato., A mediana é apenas o número do meio: 20.

às vezes os dois serão o mesmo número. Por exemplo, o conjunto de dados 1, 2, 4, 6, 7 tem uma média de 1 + 2 + 4 + 6 + 7 / 5 = 4 e uma mediana (média) de 4.média vs média: Qual é a diferença?

quando você começou em matemática, você provavelmente foi ensinado que uma média era uma quantidade “média” para um conjunto de números. Você somou os números, divididos pelo número de itens que você pode e voilá! ficas com a média. Por exemplo, a média de 10, 5 e 20 é:

10 + 6 + 20 = 36 / 3 = 12.,

The you started studying statistics and all of a sudden the “average” is now called The mean. O que houve? A resposta é que eles têm o mesmo significado(eles são sinônimos).

Que Disse, tecnicamente, a palavra média é curta para a média aritmética. Usamos palavras diferentes em estatísticas, porque há vários tipos diferentes de meios, e todos eles fazem coisas diferentes.

específico “significa” comumente usado em estatísticas

você provavelmente vai encontrar estes na sua classe stats., Eles têm significados muito estreitos:

  • média da distribuição de amostragem: usado com distribuições de probabilidade, especialmente com o Teorema do Limite Central. É uma média de um conjunto de distribuições.média da amostra: o valor médio numa amostra.média da população: o valor médio numa população.Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, 1962.

    outros tipos

    Existem outros tipos de meios, e você vai usá-los em vários ramos da matemática., A maioria tem aplicações muito estreitas em campos como finanças ou física; se você está em estatísticas elementares você provavelmente não vai trabalhar com eles.

    estes são alguns dos tipos mais comuns que você vai encontrar. média ponderada.média harmónica.média geométrica.média aritmética-geométrica.média quadrada da raiz quadrada da média quadrática.média Heroniana.média gráfica

  1. média ponderada

    estas são bastante comuns nas estatísticas, especialmente quando se estudam populações., Em vez de cada ponto de dados contribuir igualmente para a média final, alguns pontos de dados contribuem mais do que outros. Se todos os pesos são iguais, então isto irá igualar a média aritmética. Há certas circunstâncias em que isso pode dar informações incorretas, como demonstrado pelo paradoxo de Simpson.

  2. Média Harmónica

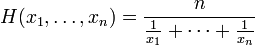
    O harmônica fórmula.

    para encontrá-lo:

    1. adicione os reciprocidade dos números no conjunto., Para encontrar um recíproco, vire a fração de modo que o numerador se torne o denominador e o denominador se torne o numerador. Por exemplo, o recíproco de 6/1 é 1/6.
    2. divida a resposta pelo número de itens no conjunto.tome o recíproco do resultado.

    a média harmônica é usada bastante na física. Em alguns casos envolvendo Taxas e rácios dá uma média melhor do que a média aritmética. Você também encontrará usos em Geometria, finanças e Ciência da computação.,

  3. média geométrica


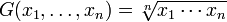
    Este tipo tem usos muito estreitos e específicos nas finanças, Ciências Sociais e Tecnologia. Por exemplo, digamos que você possui ações que ganham 5% no primeiro ano, 20% no segundo ano, e 10% no terceiro ano. Se você quer saber a taxa média de Retorno, você não pode usar a média aritmética. Por quê? Porque quando você está encontrando taxas de Retorno você está multiplicando, não adicionando. Por exemplo, o primeiro ano que você está multiplicando por 1,05.,

  4. média aritmética-geométrica

    isto é usado principalmente no cálculo e na computação de máquinas (ou seja, como o básico para muitos cálculos de computador). Está relacionado com o perímetro de uma elipse. Quando foi desenvolvido pela primeira vez por Gauss, foi usado para calcular órbitas planetárias. A aritmética-geométrica é (não surpreendentemente!) uma mistura das médias aritmética e geométrica. A matemática é bastante complicada, mas você pode encontrar uma explicação relativamente simples da matemática aqui.,

  5. Root-Mean Square

    It is very useful in fields that study sine waves, like electrical engineering. Este tipo particular também é chamado de média quadrática. Ver: Quadratic Mean / Root Mean Square.

  6. média Herónica

    usada na geometria para encontrar o volume de um frustum piramidal. Um frustum piramidal é basicamente uma pirâmide com a ponta cortada.

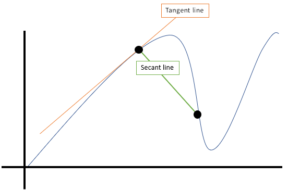
  7. média gráfica

    outro nome para o declive da linha secante: o equivalente da taxa média de variação entre dois pontos.,

Qual é o modo?

o modo é o número mais comum em um conjunto. Por exemplo, o modo neste conjunto de números é 21:
21, 21, 21, 23, 24, 26, 26, 28, 29, 30, 31, 33Qual é a mediana?

a mediana é o número médio num conjunto de dados. Para encontrar a mediana, listar seus pontos de dados em ordem ascendente e, em seguida, encontrar o número do meio., O número médio é de 28 como existem 4 números abaixo e 4 números acima:
23, 24, 26, 26, 28, 29, 30, 31, 33

Como encontrar a média, moda e mediana ao lado: Passos

Como encontrar a média, a mediana e o modo de operação: MODO

Como encontrar a média, moda e mediana: SIGNIFICA

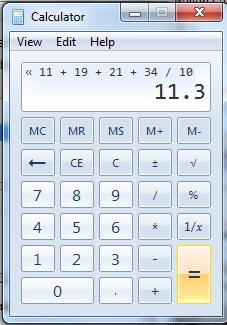
Dividindo a soma pelo número de itens para encontrar a média.

como encontrar a média, mediana e modo: mediana

Se teve um número ímpar no Passo 3, Vá para o Passo 5. Se tiver um número par, vá para o Passo 6.,dica: você pode ter mais de um modo. Por exemplo, o modo de 1, 1, 5, 5, 6, 6 1, 5 e 6.

como a explicação? Confira o manual de estatísticas praticamente enganadoras, que tem centenas de soluções passo a passo, assim como este!

SPSS mediana do modo médio

para encontrar a mediana do modo médio SPSS, terá de usar a página de Frequência. Parece um pouco contra-intuitivo, mas a página de estatísticas descritivas não lhe dá a opção de encontrar o modo ou a mediana.,

SPSS tem uma interface muito semelhante à Microsoft Excel. Portanto, se você já usou o Microsoft Excel antes, você vai se adaptar rapidamente ao SPSS.

média do modo SPSS mediana: passos

Assista ao vídeo ou leia os passos abaixo:

por favor aceite estatísticas, cookies de marketing para ver este vídeo.

Amostra Pergunta: encontrar a mediana do modo de SPSS médio para o seguinte conjunto de dados: 20,23,35,66,55,66

Passo 1: SPSS aberto. No ” What would you like to do?”caixa de diálogo, clique no botão de rádio” digite em dados “e, em seguida, clique em” OK.”Uma nova folha de trabalho vai abrir., Nota: Se você optou por sair da primeira tela de ajuda, você pode não ver esta opção. Nesse caso, comece pelo Passo 2.

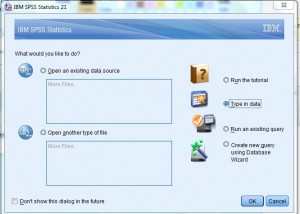
Step 2: Digite seus dados na planilha. Você pode digitar os dados em uma coluna ou várias colunas se você tiver vários conjuntos de dados. Para este exemplo, tipo 20, 23, 35, 66, 55, 66 na coluna 1. Não deixe espaços entre os dados (ou seja, não deixe linhas vazias).

Passo 2: Clique em” analisar”,” sobrevoar “estatísticas descritivas” e, em seguida, clique em “frequências”.,”

Passo 3: Clique em ” estatísticas “e, em seguida, assinale as caixas” média”,” modo “e ” mediana”.”Clique em” Continuar ” duas vezes (selecione “Nenhum” como o tipo de gráfico na segunda janela).nota :em algumas versões do SPSS, você só pode ter que clicar em “Continue” uma vez e pode não lhe dar uma opção para o tipo de gráfico.

os resultados de frequência aparecerão como resultado. A parte superior da saída irá mostrar a média, o modo e a mediana.

Se descer, a tabela de frequências também lhe mostrará o modo., O modo é definido nas estatísticas como o número com a maior frequência (para este conjunto de dados de amostra, o número que aparece mais é 66, com dois resultados na coluna de frequência).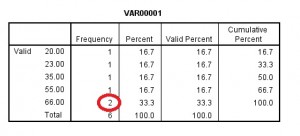

TI 83 Média, Mediana, e o Modo

Encontrar a TI 83 médio ou TI 83 mediana a partir de uma lista de dados pode ser realizado de duas formas: inserindo uma lista de dados, ou usando a tela inicial para digitar os comandos., Usar a funcionalidade da lista é tão fácil como introduzir os dados na tela inicial, e tem a vantagem adicional de que você pode usar os dados para outros fins depois de ter calculado a sua média, modo e mediana (por exemplo, você pode querer criar um histograma TI 83).

os Passos para a Média, moda e Mediana da TI 83

Assista o vídeo para a média e a mediana ou leia os passos abaixo (para o modo de ver esta nota):

por Favor, aceite as estatísticas, marketing cookies para assistir a este vídeo.

Passo 1: Introduza os dados acima numa lista., Pressione o botão STAT e, em seguida, pressione ENTER. Introduza o primeiro número (1250), e depois carregue em ENTER. Continue a introduzir os números, carregando no botão ENTER após cada entrada.Passo 2: Pressione o botão STAT.

Passo 3: Carregue no botão direito para realçar o “Calc.”

Passo 4: Carregue em ENTER para escolher “1-Var Stats” e depois escreva no nome da lista. Por exemplo, para entrar L1 press e .Passo 5: Carregue em ENTER novamente. A calculadora vai devolver a média, X. Para esta lista de dados, a média TI 83 é 884,05 pés (arredondada às três casas decimais). Passo 6: seta para baixo até ver ” Med.,”Esta é a mediana TI 83; para os dados acima, a mediana é de 813,05 pés.

Nota: O TI-83 plus não tem uma função built in mode, mas uma vez que você entrou na sua lista, é muito fácil de identificar o modo: é apenas o número que ocorre mais frequentemente no conjunto. Não tens a certeza? Leia mais sobre o modo aqui.é isso!perdeu o seu guia? Faça o Download de um novo aqui no site de TI.

——————————————————————————

Necessita de ajuda com a lição de casa, ou a pergunta de teste?, Com o estudo Chegg, você pode obter soluções passo a passo para suas perguntas de um especialista no campo. Os seus primeiros 30 minutos com um tutor Chegg são grátis!