Triângulo Figura Ângulo-Lado-Ângulo (ASA)
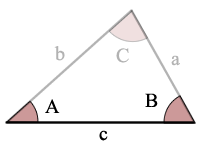
A = ângulo de Uma
B = ângulo B
C = ângulo C
a = lado a
b = lado b
c = lado c
P = perímetro
s = semi-perímetro
K = área
r = raio do círculo inscrito
R = raio do círculo circunscrito
Calculadora de Uso
Cada opção de cálculo, mostrado abaixo, tem sub-marcas que lista a seqüência de métodos utilizados nesta calculadora para resolver o desconhecido ângulo e lado valores, incluindo a Soma dos Ângulos de um Triângulo, Lei dos Senos e Lei dos Cossenos., Estas não são as únicas sequências que você poderia usar para resolver estes tipos de problemas.
- Veja também estes Trigonometria Calculadoras:
- Lei dos Cossenos Calculadora
- Direito de Sines Calculadora
Resolução de Triângulo Teoremas
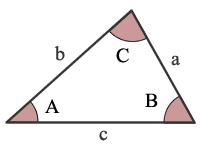
AAA é o Ângulo, Ângulo, Ângulo
Especificando os três ângulos de um triângulo não identifica exclusivamente um triângulo. Portanto, a especificação de dois ângulos de um tringle permite que você calcule apenas o terceiro ângulo., dados os tamanhos de 2 ângulos de um triângulo, pode calcular o tamanho do terceiro ângulo. O total será igual a 180 ° ou π radianos.
C = 180° – A – B (em graus)
C = π – A – B (em radianos)
AAS é o Ângulo, Ângulo, Lado
de acordo com o tamanho de 2 ângulos e 1 do lado oposto um do dado ângulos, pode-se calcular os tamanhos das restantes 1 ângulo e 2 laterais.
use a regra da Soma dos ângulos para encontrar o outro ângulo, então
use a Lei de Sines para resolver para cada um dos outros dois lados.,
ASA é Ângulo, lado, ângulo
dado o tamanho de 2 ângulos e o tamanho do lado que está entre esses 2 ângulos você pode calcular OS tamanhos dos restantes 1 ângulo e 2 lados.
use a regra da Soma dos ângulos para encontrar o outro ângulo, então
use a Lei de Sines para resolver para cada um dos outros dois lados.,
CU (ou SSA) é o Ângulo, Lado, Lado
de acordo com o tamanho de 2 lados (a e c, onde uma < c) e o tamanho do ângulo de Um que não está entre os 2 lados, você pode ser capaz de calcular os tamanhos das restantes 1 lado e 2 ângulos, dependendo das condições a seguir.,f Cossenos para resolver para cada um dos outros dois ângulos
presente 2 soluções completas
Exemplo: 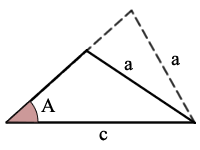
sin(A) = A/c, existe um possível triângulo
usar A Lei dos Senos para resolver um ângulo, C
use a Soma dos Ângulos Regra para encontrar o outro ângulo, B
usar A Lei dos Senos para resolver para a última lado, b
Exemplo: 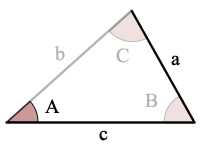
sin(A) > a/c, não há possíveis triângulos
Aviso de Erro: sin(A) > a/c por isso não há soluções, não de triângulo!,
Exemplo: 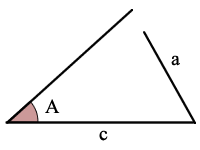
SAS é Lado, Ângulo, Lado
de acordo com o tamanho de 2 lados c e a) e o tamanho do ângulo B que está entre os 2 lados, você pode calcular os tamanhos das restantes 1 lado e 2 ângulos.
usar A Lei dos Cossenos para resolver para o lado restante, b
determinar de que lado, a ou c, é menor e usar a Lei dos Senos para resolver para o tamanho do ângulo oposto, A ou C, respectivamente.,
use a regra da Soma dos ângulos para encontrar o último ângulo
SSS é Lado, Lado, Lado
dadas as dimensões dos 3 lados você pode calcular as dimensões de todos os 3 ângulos no triângulo.
use a lei dos cossenos para resolver para os ângulos. Você também pode usar a regra da Soma dos ângulos para encontrar o ângulo final uma vez que você conhece 2 deles.,sin-1
Lei dos Cossenos
Se a, b e c são os comprimentos dos catetos de um triângulo oposto para os ângulos A, B e C, respectivamente; em seguida, a lei dos cossenos estados:
a2 = c2 + b2 – 2bc cos A, a solução para os cos A cos A = ( b2 + c2 – a2 ) / 2bc
b2 = a2 + c2 – 2ca cos B, a solução para os cos B cos B = ( c2 + a2 – b2 ) / 2ca
c2 = b2 + a2 – 2ab cos C, a solução para os cos C cos C = ( a2 + b2 – c2 ) / 2ab
de problemas, por exemplo, para um ângulo, A = cos-1
Outras Triângulo Características
Triângulo de perímetro, P = a + b + c
Triângulo semi-perímetro, s = 0.,5 * (a + b + c)
área do Triângulo, K = √
o Raio do círculo inscrito no triângulo, r = √
o Raio do círculo circunscrito em torno de triângulo, R = (abc) / (4 K)
Referências Leitura Adicional
Weisstein, Eric W. “BUNDA Teorema.”From MathWorld– A Wolfram Web Resource. Teorema do rabo.
Math is Fun-Solving SAS Triangles
















Deixe uma resposta