Mostrar aviso móvel mostrar todas as notas esconder todas as notas
a Secção 3-1 : Equações Paramétricas e Curvas
este ponto (tanto em Cálculo I e Cálculo II) vimos quase que exclusivamente em funções na forma \(y = f\left( x \right)\) ou \(x = h\left( x \right)\) e quase todas as fórmulas que desenvolvemos exigir que as funções de estar em uma destas duas formas. O problema é que nem todas as curvas ou equações que gostaríamos de ver caem facilmente nesta forma.
Tome, por exemplo, um círculo. É bastante fácil escrever a equação de um círculo centrado na origem com raio \(r\).,
\
no entanto, nunca seremos capazes de escrever a equação de um círculo como uma única equação em qualquer das formas acima. Claro que podemos resolver para \(x\) ou \(y\) como as duas fórmulas seguintes mostram
\
mas existem de facto duas funções em cada uma delas. Cada fórmula dá uma porção do círculo.
\
infelizmente, normalmente estamos trabalhando em todo o círculo, ou simplesmente não podemos dizer que vamos estar trabalhando apenas em uma parte dele. Mesmo que possamos limitar as coisas a apenas uma destas porções, a função ainda é frequentemente bastante desagradável de trabalhar.,
\
esta terceira variável é normalmente denotada por \(t\) (como fizemos aqui) mas não tem de ser, claro. Às vezes vamos restringir os valores de \(t\) que vamos usar e em outras vezes não vamos. isso muitas vezes será dependente do problema e apenas o que estamos tentando fazer.
para ajudar a visualizar apenas o que uma curva paramétrica é fingir que temos um grande tanque de água que está em movimento constante e nós deixamos cair uma bola de pingue-pongue no tanque., O ponto \(\left( {x,y} \right) = \left( {f\left( t \right),g\left( t \right)} \right)\), então, representar a localização da bola de pingue-pongue no tanque no momento \(t\) e a curva paramétrica será um rastreamento de todos os locais da bola de pingue-pongue. Note que esta não é sempre uma analogia correta, mas é útil inicialmente para ajudar a visualizar apenas o que é uma curva paramétrica.esboçar uma curva paramétrica nem sempre é uma coisa fácil de fazer. Vamos dar uma olhada em um exemplo para ver uma maneira de desenhar uma curva paramétrica., Este exemplo também ilustrará porque este método não é geralmente o melhor.
neste ponto a nossa única opção para desenhar uma curva paramétrica é escolher valores de \(t\), ligá-los às equações paramétricas e depois desenhar os pontos. Então, vamos ligar alguns \(t\)’s.,x\)
The first question that should be asked at this point is, how did we know to use the values of \(t\) that we did, especially the third choice?, Infelizmente, neste momento, não existe uma verdadeira resposta a esta pergunta. Nós simplesmente escolher \(t\) ‘ S até que estamos bastante confiantes de que temos uma boa idéia de como a curva se parece. É este problema com a escolha de valores” bons ” de \(t\) que fazem deste método de esboçar curvas paramétricas uma das escolhas mais pobres. Às vezes não temos escolha, mas se temos escolha devemos evitá-la.
discutiremos um método alternativo de graficação em exemplos posteriores que ajudarão a explicar como estes valores de \(t\) foram escolhidos.,temos mais uma ideia para discutir antes de esboçarmos a curva. Curvas paramétricas têm uma direção de movimento. A direcção do movimento é dada pelo aumento \(t\). Então, ao traçar curvas paramétricas, também incluímos setas que mostram a direção do movimento. Muitas vezes vamos dar o valor de \(t\) que deu pontos específicos no gráfico, bem como para deixar claro o valor de \(t\) que deu esse ponto em particular.
Aqui está o esboço desta curva paramétrica.
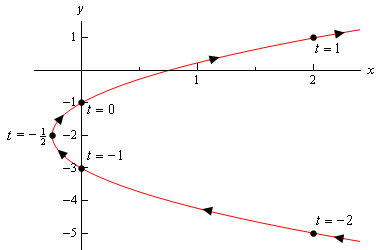
assim, parece que temos uma parábola que se abre para a direita.,
Antes de terminar este exemplo há um ponto um tanto importante e sutil que precisamos discutir primeiro. Observe que nos certificamos de incluir uma parte do sketch à direita dos pontos correspondentes a \(t = – 2\) e \(t = 1\) para indicar que existem porções do sketch lá. Se tivéssemos simplesmente parado o sketch nesses pontos, estaríamos a indicar que não havia nenhuma parte da curva à direita desses pontos e que, claramente, haverá. Não calculámos nenhum desses pontos.,
Este pode parecer um ponto sem importância, mas como veremos no próximo exemplo é mais importante do que pensamos.
Antes de abordar uma maneira muito mais fácil de esboçar este gráfico vamos primeiro abordar a questão dos limites do parâmetro. No exemplo anterior não tínhamos quaisquer limites no parâmetro. Sem Limites no parâmetro o grafo continuará em ambas as direções como mostrado no sketch acima.
muitas vezes teremos Limites no parâmetro no entanto e isso afetará o esboço das equações paramétricas., Para ver este efeito vamos olhar uma ligeira variação do exemplo anterior.
Note que a única diferença aqui é a presença dos limites em \(t\). Todos estes limites fazem é dizer-nos que não podemos tomar qualquer valor de \(t\) fora deste intervalo. Portanto, a curva paramétrica será apenas uma porção da curva acima. Aqui está a curva paramétrica para este exemplo.,
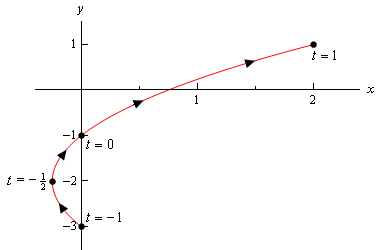
Observe que com este esboço que começou e parou o esboço de direito sobre os pontos de origem a partir do ponto final do intervalo de \(t\)’s. Contraste isso com o esboço no exemplo anterior, onde tivemos uma parte do desenho para a direita do “início” e “fim” de pontos que calculamos.
neste caso, a curva começa em \(t = – 1\) e termina em \(t = 1\), enquanto que no exemplo anterior a curva não começou na maioria dos pontos certos que calculámos., Precisamos ser claros em nossos esboços se a curva começa / termina em um ponto, ou se esse ponto foi simplesmente o primeiro / último que computamos.
Agora é hora de dar uma olhada em um método mais fácil de esboçar esta curva paramétrica. Este método usa o fato de que em muitos casos, mas não todos, podemos realmente eliminar o parâmetro das equações paramétricas e obter uma função envolvendo apenas \(x\) e \(y\). Às vezes chamaremos a isto a equação algébrica para diferenciá-la das equações paramétricas originais., Haverá dois pequenos problemas com este método, mas será fácil resolver esses problemas. É importante notar, no entanto, que nem sempre seremos capazes de fazer isso.
apenas como eliminamos o parâmetro dependerá das equações paramétricas que temos. Vamos ver como eliminar o parâmetro para o conjunto de equações paramétricas com as quais temos trabalhado até este ponto.obter um esboço da curva paramétrica uma vez eliminado o parâmetro parece bastante simples. Tudo o que precisamos fazer é graficar a equação que encontramos eliminando o parâmetro., No entanto, como já foi referido, existem dois pequenos problemas com este método. A primeira é a direção do movimento. A equação que envolve apenas \(x\) e \(y\) não irá dar a direcção do movimento da curva paramétrica. Este é geralmente um problema fácil de corrigir no entanto. Vamos dar uma olhada rápida nas derivadas das equações paramétricas do último exemplo. Eles são,
\
Note que a derivada \(x\) não é tão útil para esta análise, pois será tanto positiva como negativa e, portanto, \(x\) será tanto aumentando e diminuindo dependendo do valor de \(t\)., Isso não ajuda com a direção, tanto quanto seguir a curva em qualquer direção exibirá tanto aumento e diminuição \(x\).
em alguns casos, apenas uma das equações, como este exemplo, irá dar a direção, enquanto em outros casos qualquer um poderia ser usado. Também é possível que, em alguns casos, ambos os derivados seriam necessários para determinar a direção. Será sempre dependente do conjunto individual de equações paramétricas.,
O segundo problema com a eliminação do parâmetro é melhor ilustrado em um exemplo, como vamos estar correndo para este problema nos exemplos restantes.Ok, esse foi um exemplo muito longo. A maioria destes tipos de problemas não são tão longos. Tivemos muito que discutir neste caso para que pudéssemos tirar algumas ideias importantes do caminho. O resto dos exemplos nesta seção não deve demorar tanto tempo para passar.
Agora, vamos dar uma olhada em outro exemplo que irá ilustrar uma ideia importante sobre equações paramétricas.,
assim, vimos nos dois últimos exemplos dois conjuntos de equações paramétricas que de alguma forma deram o mesmo grafo. No entanto, como eles traçaram o gráfico um número diferente de vezes nós realmente precisamos pensar neles como curvas paramétricas diferentes, pelo menos de alguma forma. Isto pode parecer uma diferença com a qual não precisamos nos preocupar, mas como veremos em seções posteriores, esta pode ser uma diferença muito importante. Em algumas das seções posteriores vamos precisar de uma curva que é traçada exatamente uma vez.,
Before we move on to other problems let’s briefly acknowledge what happens by changing the \(t\) to an nt in these types of parametric equations. Quando estamos lidando com equações paramétricas envolvendo apenas sines e cossenos e ambos têm o mesmo argumento se mudarmos o argumento de \(t\) para nt simplesmente mudamos a velocidade com que a curva é traçada. Se \(n > 1\), vamos aumentar a velocidade e a se \(n < 1\), vamos diminuir a velocidade.
vamos dar uma olhada em mais alguns exemplos.,
a este ponto vimos exemplos que iriam traçar o gráfico completo que obtivemos eliminando o parâmetro se pegássemos uma grande gama suficiente de \(t\)’s. No entanto, no exemplo anterior já vimos que este nem sempre será o caso. É mais do que possível ter um conjunto de equações paramétricas que continuamente traçam apenas uma parte da curva. Normalmente, podemos determinar se isto irá acontecer procurando limites em \(x\) e \(y\) que são impostos por meio da equação paramétrica.,
usaremos muitas vezes equações paramétricas para descrever o caminho de um objeto ou partícula. Vejamos um exemplo disso.
devemos dar um pequeno aviso neste ponto. Por causa das ideias envolvidas nelas, concentrámo-nos em curvas paramétricas que refizeram porções da curva mais de uma vez. No entanto, não fique demasiado preso à ideia de que isto irá sempre acontecer. Muitos, se não a maioria das curvas paramétricas, só vão traçar uma vez. O primeiro que analisámos é um bom exemplo disso. Essa curva paramétrica nunca irá repetir nenhuma parte de si mesma.,
Há um tópico final a ser discutido nesta seção antes de seguir em frente. Até agora começamos com equações paramétricas e eliminamos o parâmetro para determinar a curva paramétrica.
no entanto, há momentos em que queremos ir para o outro lado. Dada uma função ou equação, podemos querer escrever um conjunto de equações paramétricas para ela. Nestes casos dizemos que parametrizamos a função.
Se tomarmos os exemplos 4 e 5 como exemplos podemos fazer isso para elipses (e, portanto, círculos)., Dada a elipse
\
um conjunto de equações paramétricas para o que seria,
\
Este conjunto de equações paramétricas vai traçar a elipse, começando pelo ponto \(\left( {a,0} \right)\) e de rastreamento em um sentido anti-horário, e vai traçar exatamente uma vez no intervalo \(0 \le t \le 2\pi \). Este é um conjunto bastante importante de equações paramétricas como ele usado continuamente em alguns assuntos com lidar com elipses e/ou círculos.
cada curva pode ser parametrizada em mais de uma maneira. Qualquer um dos seguintes também parametrizará a mesma elipse.,
\
a presença do \(\omega \) irá mudar a velocidade que a elipse gira como vimos no exemplo 5. Note também que os dois últimos vão traçar elipses com uma direção de movimento no sentido horário (você pode querer verificar isso). Note também que eles não vão começar todos no mesmo lugar (se pensarmos em \(t = 0\) como o ponto de partida que é).
Existem muitas mais parametrizações de uma elipse, é claro, mas você tem a idéia. É importante lembrar que cada parametrização irá traçar a curva uma vez com um intervalo potencialmente diferente de \(t\)’s., Cada parametrização pode rodar com diferentes direções de movimento e pode começar em diferentes pontos.
Você pode achar que você precisa de uma parametrização de uma elipse que começa em um determinado lugar e tem direção de movimento e por isso agora você já sabe que, com algum trabalho, você pode escrever um conjunto de equações paramétricas que vai dar-lhe o comportamento que você está depois.
Agora, vamos escrever um par de outras parametrizações importantes e todos os comentários sobre a direção do movimento, ponto de partida, e intervalo de \(t\)’S para um traço (se aplicável) ainda são verdadeiros.,
primeiro, porque um círculo não é nada mais do que um caso especial de uma elipse, podemos usar a parametrização de uma elipse para obter as equações paramétricas de um círculo centrado na origem do raio \(r\) também. Uma forma possível para parametrizar um círculo é,
\ \
neste momento, pode não parecer tão útil para fazer uma parametrização de uma função como esta, mas há muitos casos em que ela realmente vai ser mais fácil, ou pode até ser necessário, para trabalhar com a parametrização em vez de a própria função., Infelizmente, quase todos estes casos ocorrem em um curso de cálculo III.
















Deixe uma resposta