Mostrar aviso móvel mostrar todas as notas esconder todas as notas
secção 4-11 : aproximações Lineares
nesta secção vamos dar uma vista de olhos a uma aplicação não de derivados mas da linha tangente a uma função. Claro, para obter a linha tangente, precisamos tomar derivados, então de alguma forma isso é uma aplicação de derivados também.
\
dê uma olhada no seguinte gráfico de uma função e sua linha tangente.
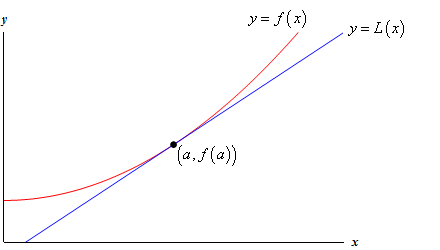
então, porque faríamos isto? Vejamos um exemplo.,
aproximações Lineares fazem um trabalho muito bom de aproximar valores de \(f\esquerda (x \direita)\) desde que permaneçamos “perto” \(x = a\). No entanto, quanto mais longe de \(x = a\) ficamos pior a aproximação é susceptível de ser. O principal problema aqui é que quão perto precisamos de ficar para \(x = a\), a fim de obter uma boa aproximação dependerá tanto da função que estamos usando quanto do valor de \(x = a\) que estamos usando. Além disso, muitas vezes não haverá uma maneira fácil de prever quão longe de \(x = A\) Podemos obter e ainda ter uma aproximação “boa”.,
Let’s take a look at another example that is actually used fairly heavily in some places.
Esta é realmente uma aproximação linear algo importante. Na óptica, esta aproximação linear é muitas vezes usada para simplificar fórmulas. Esta aproximação linear também é usada para ajudar a descrever o movimento de um pêndulo e vibrações em uma corda.
















Deixe uma resposta