vetores são extensivamente úteis na ciência para descrever qualquer coisa que tenha tanto uma direção como uma magnitude. Eles são geralmente desenhados com a ajuda de setas pontiagudas, cujo comprimento representará a magnitude do vetor. O passe de um quarterback é o exemplo simples porque ele tem a direção geralmente em algum ponto do campo e uma magnitude. Às vezes temos que lidar com dois vetores juntos trabalhando em algum objeto. Nesses casos, os ângulos entre esses vetores são importantes., Este tópico explicará o ângulo entre duas fórmulas de vetores, bem como exemplos. Aprendamos!
conceito de vetores
fora do campo, vetores podem ser usados para representar qualquer número de objetos físicos ou atividades. Por exemplo. O vento, por exemplo, é uma quantidade vectorial. É porque em um determinado local tem uma direção, bem como a magnitude. Podemos fazer um mapa de fluxo de ar em qualquer ponto do tempo, então, desenhando os vetores de vento para uma série de diferentes localizações geográficas.
muitas propriedades de objetos em movimento também são tipo de vetores., Na bola de bilhar, seu Vetor de velocidade descreve seu movimento. Ele mostra a direção das marcas de seta vectorial como a direção do movimento, e o comprimento do vetor representa a velocidade da bola.
o momento da bola de bilhar é também um exemplo de quantidade vectorial. Como é igual a massa vezes velocidade. Portanto, o vetor de momento das esferas na mesma direção que seu Vetor de velocidade. E a magnitude do vetor de momento será o produto multiplicador da velocidade da bola e sua massa.,
em termos matemáticos, um vetor é qualquer objeto que tem uma magnitude e direção definíveis. Como os vetores não são os mesmos que as linhas ou formas padrão, precisamos usar algumas fórmulas especiais para encontrar ângulos entre eles.
A Fórmula para o Ângulo entre Dois Vetores
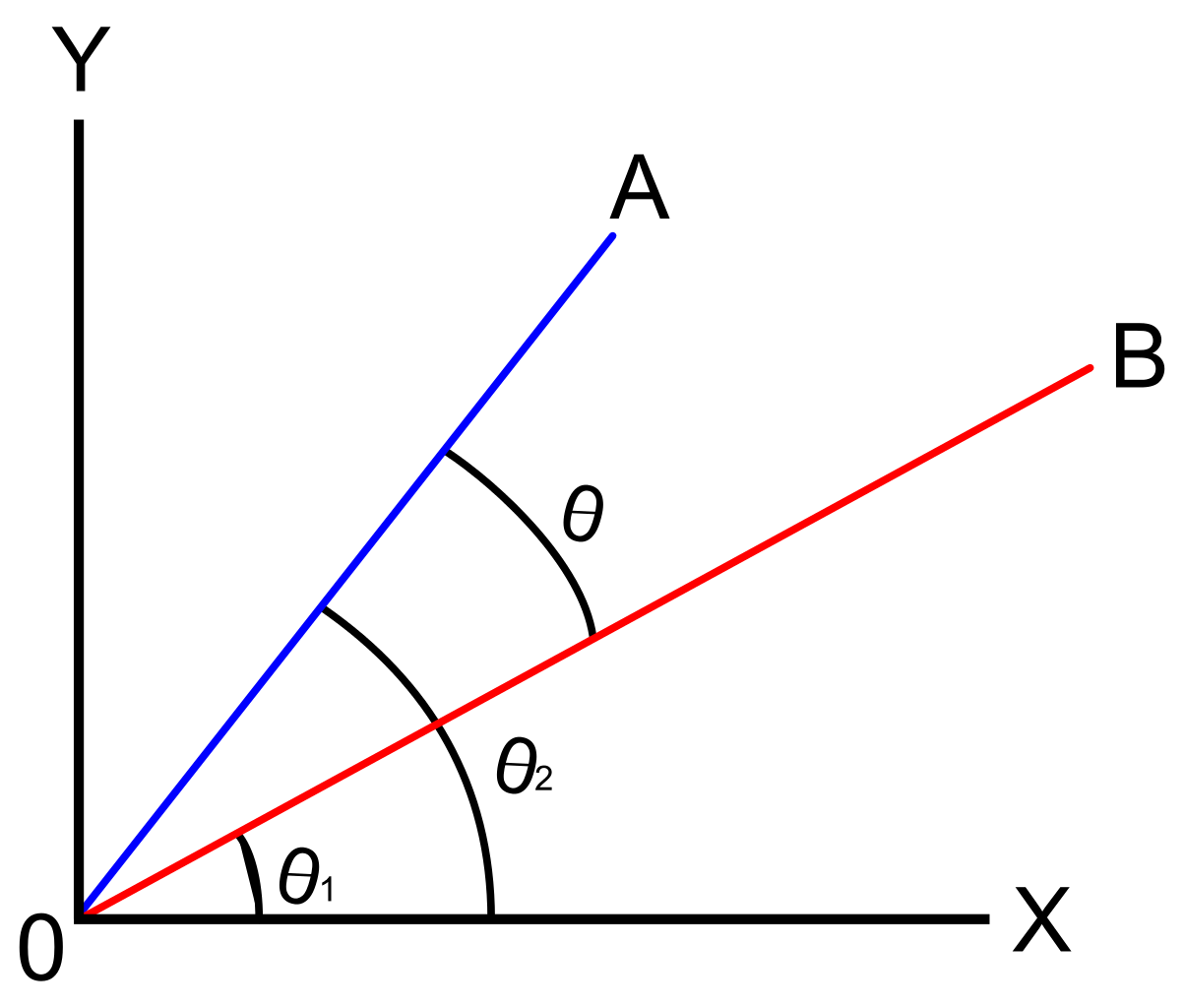
O ângulo entre dois vetores será adiada por um único ponto, que é chamado como o menor ângulo em que temos de virar um dos vetores para a posição de co-direcional com outro vetor.,
a discussão sobre ângulos de direção de vetores centra-se em encontrar o ângulo de um vetor em relação ao eixo x positivo. Isto irá focar no ângulo entre dois vetores na posição padrão. Um vetor é dito estar em posição padrão se seu ponto inicial é a origem (0, 0).
Se os dois vetores são assumidos como a e b, então o ponto criado é definido como A.B. vamos assumir que estes dois vetores estão separados por ângulo \(\theta\). Para saber qual é a medição do ângulo que vamos resolver com a ajuda da fórmula dada:
conhecemos o produto Ponto:
\(\vec{a}.,\vec{B} =|\vec{a}||\vec{B}|cos\theta\)
Agora, o ângulo entre duas fórmulas de vetores é:
\(\theta = cos^{-1}\frac{\vec{a}.\vec{B}} {|\vec{a}||\vec{B}/}\)
Onde \\(theta\) é o ângulo entre os vectores a e B.
Resolvido Exemplos de Ângulo entre Dois Vetores Fórmula
Q. 1: Calcular o ângulo entre dois vetores 3i + 4j – k e 2i – j + k.
Solução: Deixar,
a = 3i + 4j – k e
b = 2i – j + k
definimos o produto escalar como:
um .b = (3i + 4j – k).(2i – j + k)
















Deixe uma resposta