a Probabilidade de rolar dois dados de seis lados dotssuch como 1, 2, 3, 4, 5 e 6 pontos em cada morrer.

Quando dois dados são lançados simultaneamente, portanto, o número de evento pode ser 62 = 36 porque cada dado de 1 a 6 número de faces. Então os resultados possíveis são mostrados na tabela abaixo.,
Probabilidade – Exemplo de espaço para dois dados (resultados):
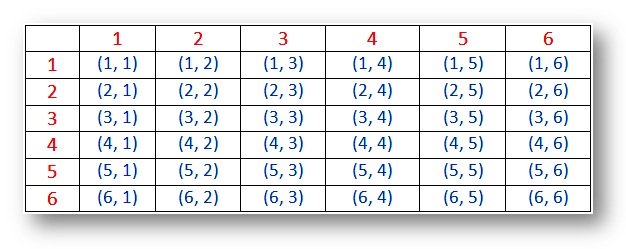
Nota:
(i) Os resultados (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) e (6, 6) são chamados de parelhas.
(ii) o par (1, 2) e (2, 1) são resultados diferentes.
problemas trabalhados envolvendo probabilidade de rolar dois dados:
1. Dois dados são lançados. Seja A, B, C os eventos de obter uma soma de 2, uma soma de 3 e uma soma de 4, respectivamente., Em seguida, mostre que
(i) a é Um evento simples
(ii) B e C são compostos de eventos
(iii) A e B são mutuamente exclusivos
Solução:
Claramente, nós temos
A = {(1, 1)}, B = {(1, 2), (2, 1)} e C = {(1, 3), (3, 1), (2, 2)}.
(i) Uma vez que a consiste em um único ponto de amostra, é um evento simples.
(ii) uma vez que tanto B Quanto C contêm mais de um ponto de amostra, Cada um deles é um evento composto.
(iii) uma vez que A ∩ B = ∅, A E B são mutuamente exclusivos.
2. Dois dados são lançados., A é o evento que a soma dos números mostrados nos dois dados é 5, e B é o evento que pelo menos um dos dados mostra um 3. os dois eventos (i) se excluem mutuamente, (ii) são exaustivos? Apresente argumentos em apoio da sua resposta.
solução:
Quando dois dados são rolados, temos n (S) = (6 × 6) = 36.
Agora, Um = {(1, 4), (2, 3), (4, 1), (3, 2)}, e
B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i) A ∩ B = {(2, 3), (3, 2)} ≠ ∅.assim, A E B não se excluem mutuamente.,
(ii) Also, a ∪ B ≠ S.
conseqüentemente, A e B não são eventos exaustivos.
Mais exemplos relacionados com as perguntas sobre as probabilidades de lançar dois dados.
3. Dois dados são lançados simultaneamente.,) um gibão
(v) obtendo uma soma de 8
(vi) obtenção de soma divisível por 5
(vii) a soma de pelo menos 11
(viii) obter um múltiplo de 3, como a soma
(ix) obtendo um total de pelo menos 10
(x) obtenção de um número par como a soma
(xi) obtenção de um número primo como a soma
(xii) a obtenção de um gibão de números pares
(xiii) obter um múltiplo de 2, em um morrer e um múltiplo de 3 por outro morrer
Solução:
Dois diferentes dados são lançados simultaneamente, sendo o número 1, 2, 3, 4, 5 e 6 em suas faces., Sabemos que em um único lançamento de dois dados diferentes, o número total de resultados possíveis é (6 × 6) = 36.
(i) obtendo seis como um produto:
Let E1 = event of getting six as a product. O número cujo produto é de seis serão E1 = = 4
Assim, a probabilidade de ofgetting ‘seis como um produto’
o Número de resultados favoráveis
P(E1) = número Total de possíveis resultados
= 4/36
= 1/9
(ii) a obtenção de soma ≤ 3:
Deixe E2 = evento de ficar soma ≤ 3., O número cuja soma ≤ 3 será E2 = = 3
Assim, a probabilidade de ofgetting ‘soma ≤ 3’
o Número de resultados favoráveis
P(E2) = número Total de possíveis resultados
= 3/36
= 1/12
(iii) a obtenção de soma ≤ 10:
Deixe E3 = evento de ficar soma ≤ 10. O número cuja soma ≤ 10 será E3 =
= 33
Assim, a probabilidade de ofgetting ‘soma ≤ 10’
o Número de resultados favoráveis
P(E3) = número Total de possíveis resultados
= 33/36
= 11/12
(iv)a obtenção de um gibão:Deixe E4 = evento de obter um gibão., O número de gibão vai ser E4 = = 6
Assim, a probabilidade de ofgetting ‘um gibão’
o Número de resultados favoráveis
P(E4) = número Total de possíveis resultados
= 6/36
= 1/6
(v)obtendo uma soma de 8:
Deixe E5 = evento de obter um total de 8. O número que é a soma de 8 será E5 = = 5
Assim, a probabilidade de ofgetting ‘a soma de 8’
o Número de resultados favoráveis
P(E5) = número Total de possíveis resultados
= 5/36
(vi)obtenção de soma divisíveis por 5:
Deixe E6 = evento de ficar soma divisível por 5., O número cuja soma divisível por 5 E6 = = 7
Assim, a probabilidade de ofgetting ‘soma divisível por 5’
o Número de resultados favoráveis
P(E6) = número Total de possíveis resultados
= 7/36
(vii)a soma de pelo menos 11:
Deixe E7 = caso de soma de pelo menos 11. Os eventos de a soma de pelo menos 11 serão E7 = = 3
Assim, a probabilidade de ofgetting ‘soma de pelo menos 11’
o Número de resultados favoráveis
P(E7) = número Total de possíveis resultados
= 3/36
= 1/12
(viii) obter amultiple de 3 como a soma:
Deixe E8 = evento de obter um múltiplo de 3, como a soma., The events of a multiple of 3 as the sum will be E8 = = 12
Therefore, probability ofgetting ‘a multiple of 3 as the sum’
Number of favorable outcomes
P ( E8)= Total of possible outcome
= 12/36
= 1/3
(ix) getting a total of atleast 10:
Let E9 = event of getting a total of atleast 10., Os eventos de um total de pelo menos 10 será E9 = = 6
Assim, a probabilidade de ofgetting ‘um total de pelo menos 10’
o Número de resultados favoráveis
P(E9) = número Total de possíveis resultados
= 6/36
= 1/6
(x) a obtenção de um evennumber como a soma:
Deixe E10 = evento de obter um número par como a soma., Os eventos de um mesmo número, conforme a soma será E10 = = 18
Assim, a probabilidade de ofgetting ‘um número par como a soma
o Número de resultados favoráveis
P(E10) = número Total de possíveis resultados
= 18/36
= 1/2
(xi) a obtenção de um primenumber como a soma:
Deixe E11 = evento de obter um número primo como a soma., Os eventos de um número primo como a soma será E11 = = 15
Assim, a probabilidade de ofgetting “um número primo como a soma’
o Número de resultados favoráveis
P(E11) = número Total de possíveis resultados
= 15/36
= 5/12
(xii) a obtenção de adoublet de números pares:
Deixe E12 = evento de conseguir um par de números., Os eventos de um gibão de números será E12 = = 3
Assim, a probabilidade de ofgetting ‘um gibão de números’
o Número de resultados favoráveis
P(E12) = número Total de possíveis resultados
= 3/36
= 1/12
(xiii) a obtenção de amultiple a 2 em um morrer e um múltiplo de 3, o outro morre:
Deixe E13 = evento de obter um múltiplo de 2, em um morrer e um múltiplo de 3, o outro morre., Os eventos de um múltiplo de 2, em um morrer e um múltiplo de 3 por outro morrer vai ser E13 = = 11
Assim, a probabilidade de ofgetting ‘um múltiplo de 2, em um morrer e um múltiplo de 3 por outro morrer’
o Número de resultados favoráveis
P(E13) = número Total de possíveis resultados
= 11/36
4. São lançados dois. Encontre (i) as probabilidades a favor de obter a soma 5, e (ii) theodds contra obter a soma 6.
solução:
sabemos que num único lançamento de dois dados, o número total de resultados possíveis é (6 × 6) = 36.
vamos ser o espaço de amostra. Então, n (S) = 36.,
(i) as probabilidades a favor de obter a soma 5:
seja E1 o evento de obter a soma 5. Em seguida,
E1 = {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒ P(E1) = 4
Portanto, P(E1) = n(E1)/n(S) = 4/36 = 1/9
⇒ odds a favor de E1 = P(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii) The odds against getting the sum 6:
Let E2 be the event of getting the sum 6. Em seguida,
E2 = {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒ P(E2) = 5
Portanto, P(E2) = n(E2)/n(S) = 5/36
⇒ probabilidades contra E2 = /P(E2) = (1 – 5/36)/(5/36) = 31/5.
5., Dois dados, um azul e um laranja, são rolados simultaneamente. Find the probability of getting
(i) equal numbers on both
(ii) two numbers appearing on them whose sum is 9.,
Solução:
Os resultados possíveis são
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
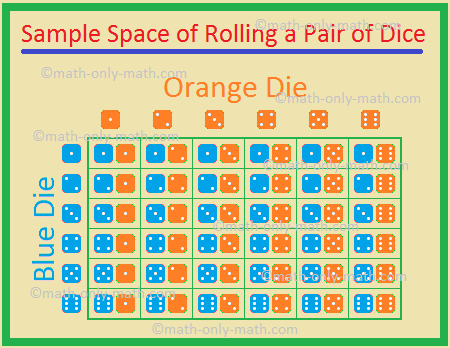
Portanto, o número total de resultados possíveis = 36.,
(i) número de resultados favoráveis para o evento e
= número de resultados com números iguais em ambos os dados
= 6 .
Então, por definição, P(E) = \(\frac{6}{36}\)
= \(\frac{1}{6}\)
(ii) Número de resultados favoráveis para o evento F
= Número de resultados em que dois números que aparecem no-los têm a soma de 9
= 4 .
Assim, por definição, P(F) = \(\frac{4}{36}\)
= \(\frac{1}{9}\).
estes exemplos ajudarão a resolver diferentes tipos de problemas com base na probabilidade de rolagem de dois dados.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















Deixe uma resposta