삼각형을 그림을 각-Side-Angle(ASA)
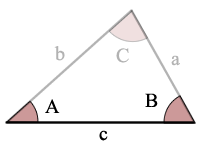
A=각
B=각 B
C=각 C
a=측
b=측 b
c=측 c
P=계
s=semi-경계
K=영역
r=의 반경을 새기는 원형
R=radius 의 제한된 원
계산기를 사용
각 계산 옵션은 아래와 같은 sub-글머리 기호는 목록의 순서에 사용되는 방법 이 계산을 해결하는 알 수 없는 각도 측 값을 포함한 합의 삼각형의 각도는,법률 시네스와 법의 사인과 코사인., 이러한 유형의 문제를 해결하는 데 사용할 수있는 유일한 시퀀스는 아닙니다.
- 을 참조하십시오 또한 이러한 삼각함수 계산:
- 법 코사인의 계산기
- 시네스의 법칙 계산기
해결하는 삼각형 Theorems
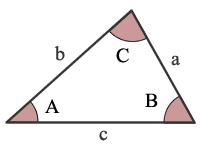
AAA 은 각 각, 각
지정하는 세 가지 각도의 삼각형을 고유하게 식별하지 않습 하나의 삼각형이다. 따라서 트링글의 두 각도를 지정하면 세 번째 각도 만 계산할 수 있습니다.,
삼각형의 2 각도의 크기가 주어지면 세 번째 각도의 크기를 계산할 수 있습니다. 합계는 180°또는 π 라디안과 같습니다.
C=180°-A-B(도)
C=π-A-B(라디안)
AAS 은 각 각도 측
어의 크기는 2 개의 각 1 면 반대의 주어진 각도를 계산할 수 있습니다 크기의 나머지 1 각도와 2 개의 측.
를 사용하여 합의 각 규칙을 찾아 다른 각도에,다음
사용의 법률 시네스에 대한 해결하기 위해 각각의 다른 두 개의 면이 있습니다.,
ASA 은 각,면,각
주어진 크기의 2 앵글 및 크기의 옆에 있는 사람들 2 각도를 계산할 수 있습니다 크기의 나머지 1 각도와 2 개의 측.
를 사용하여 합의 각 규칙을 찾아 다른 각도에,다음
사용의 법률 시네스에 대한 해결하기 위해 각각의 다른 두 개의 면이 있습니다.,
엉덩이(SSA)은 각도 측에,부작
주어진 크기의 2 양측(c 는<c)크기의 각도에 없는 사람들 2 양측할 수 있습을 계산하는 크기의 나머지 1 및 2 개의 각도에 따라 다음의 조건입니다.,f 사인과 코사인에 대한 해결하기 위해 각각 다른 두 가지의 앵글
현재 2 전체 솔루션
예: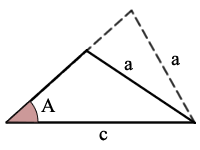
sin(A)=a/c,거기에 하나의 가능한 삼각형
사용의 법률 시네스에 대한 해결하기 위해,각도 C
를 사용하여 합의 각 규칙을 찾아 다른 각도,B
사용의 법률 시네스에 대한 해결하기 위해 마지막으면,b
예: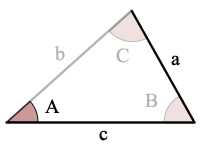
sin(A)>a/c, 이 없 가능한 삼각형
오류를 알 수 있:sin(A)>a/c 그래서 솔루션은 없습니다없각한다.,
예: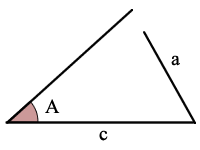
SAS 은 측 각도 측
주어진 크기의 2 양측(c)크기의 각 B 는 사람이 2 양측 당신을 계산할 수 있습니다 크기의 나머지 1 및 2 각도입니다.
를 사용하여 법률의 사인과 코사인에 대한 해결하기 위해 남은 측 b
결정하는 쪽 또는 c,은 가장 작은 사용의 법률 시네스에 대한 해결하기 위해 크기의 각도,C 각각합니다.,
를 사용하여 합의 각 규칙을 찾으려면 각
SSS 면,측면,측
주어진 크기는 3 개의 측면에 당신을 계산할 수 있습니다 크기의 모든 3 개의 각도에 삼각형이다.
각도에 대해 해결하기 위해 코사인의 법칙을 사용합니다. 각도 규칙의 합을 사용하여 그 중 2 개를 알게되면 최종 각도를 찾을 수도 있습니다.,sin-1
법률의 사인과 코사인
경우에는 a,b 및 c 은 길이의 다리의 삼각형을 반대하는 각도 A,B,C 각각 다음 법률의 사인과 코사인다:
a2=c2+b2-2bc cos,해결에 대한 cos,cos=(b2+c2-a2) /2bc
b2=a2+c2-2ca cos B,해결에 대한 cos B,cos B=(c2+a2-b2)/2ca
c2=b2+a2-2ab cos C,해결에 대한 cos C,cos C=(a2+b2-c2)/2ab
해결,예를 들어,각도 A=cos-1
기타 삼각형적 특성
삼각형의 둘레에,P=a+b+c
삼각형은 반 경계,s=0.,5*(a+b+c)
트라이앵글 지역,K=√
반경을 새기는 원형에 삼각형,r=√
반경을 제한한 주위에 원형 삼각형,R=(abc)/(4K)
참조/추가 읽기
Weisstein,에릭 W.”엉덩이 정리했습니다.”MathWorld 에서-볼프람 웹 자원. 엉덩이 정리.수학은 재미 있습니다-Sas 삼각형을 푸는 것
















답글 남기기