남자. 나는 어떻게 든 당신이 말하는 것을 좋아한다고 느낍니다.
Soc. 그리고 나,메노,내가 말하는 것과 같습니다.
플라톤의 메노에서
단위 제곱의 대각선의 길이는 2 의 제곱근과 같습니다.
단위 제곱의 대각선의 길이는√2 와 같습니다. 글쎄,이것은 정말 좋은 소식이 아닙니다. 피타고라스의 정리를 접한 모든 사람들은 그 사실을 알고 있습니다., 길이 1 의 다리가있는 이등변 직각 삼각형에서 빗변은 피타고라스 정리에 따르면-12+12=(빗변)2-실제로 길이√2 입니다. 이 페이지에 대한 동기는 그 사실 자체가 아니라 유명한 정리에 대한 의지없이 그것을 보여주는 방법입니다. 실제로,피타고라스의 정리가 남용되었을 수도 있다고 주장 할 수 있으며,호기심 많은 예를 참조하십시오.
인수는 다시 그림을 그려진에 의해 소크라테스는 플라톤의 메노 되어 있을 수 있습을 피타고라스는 자신만,후자는 살았는 이전 세기.,
대화 상자에서 소크라테스는 자신의 일반적인 방법으로,이 젊은 슬레이브에게 건설을 사각형의 두 번의 영역이 지정된 one:
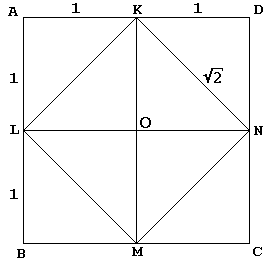
주어진 광장 KLMN 센터 O 은 첫 번째 절단하여 대각선으로 4 개의 삼각형 동등합니다. 소크라테스는이 삼각형을 빗변에 각각 반영하는 것처럼 KLMN 을 더 큰 사각형 ABCD 에 내장합니다. 노예는 그 때 인정한다-그리고 누가하지 않을 것인가? -그 정사각형 ABCD 는 정사각형 KLMN 보다 두 배나 큽니다.
진실은,socrates’s square ABCD 측에서 4 를 측정했는데,square KLMN 은 8 의 면적을 가졌다., 우리가 측면 2 의 정사각형 ABCD(따라서 영역 4)로 시작할 때,정사각형 KLMN 은 2 의 면적을 가질 것임이 분명합니다.
이제 일반적으로 양수 A 의 경우√A 는 정사각형이 A 인 숫자로 정의됩니다.
(√A)2.
반면에 영역의 모든 학생은 측면 b 의 제곱의 면적이 b2 와 같다는 것을 알고 있습니다. 면적 A 를 갖는 정사각형의 변이 정확히√A. 우리는 정사각형의 변이 klmn 이√2 와 같다고 결론을 내립니다. 인수의 중심점은 다이어그램에서 KN 이 이중 역할을한다는 사실입니다., 정사각형 KLMN 의 측면 중 하나 인 것 외에도 정사각형 OKDN 의 대각선 역할을합니다. 후자는 물론 우리의 주장을 증명하는 단위 사각형입니다.(조금 다른 관점에서 동일한 에피소드가 다른 곳에서 언급됩니다.)
















답글 남기기