벡터는 광범위하게 유용한 과학에서 설명하는 아무것도 모두 갖는 방향뿐만 아니라 크기이다. 그것들은 일반적으로 뾰족한 화살표의 도움으로 그려지며,길이는 벡터의 크기를 나타낼 것입니다. 쿼터백과 간단한 예제를 가지고 있기 때문에 방향으로 일반적으로 어딘가에 다운 필리고 크기. 때로는 일부 객체에서 작업하는 두 벡터를 함께 처리해야합니다. 이러한 경우 해당 벡터 사이의 각도가 중요합니다., 이 항목에서는 예제뿐만 아니라 두 벡터 수식 사이의 각도를 설명합니다. 우리가 그것을 배울 수 있습니다!
벡터의 개념
분야,벡터를 나타내는 데 사용될 수 있는 어떤 숫자의 물리적 객체 또는 활동입니다. 예를 들면. 예를 들어 바람은 벡터링 수량입니다. 그것은 어떤 주어진 위치에서 방향뿐만 아니라 크기를 가지고 있기 때문입니다. 우리가 만들 수 있습니다지도의 기류는 어떤 시점에서,다음에 의하여,그림 바람 벡터의 수는 다른 지리적 위치.
움직이는 물체의 많은 속성들도 일종의 벡터입니다., 당구 공에서 속도 벡터는 움직임을 설명합니다. 벡터 화살표 표시의 방향을 동작 방향으로 표시하고 벡터의 길이는 볼의 속도를 나타냅니다.
당구 공의 운동량도 벡터리 수량의 예입니다. 그것은 질량 배 속도와 동일하기 때문에. 따라서 볼 포인트의 운동량 벡터는 속도 벡터와 같은 방향입니다. 그리고 운동량 벡터의 크기는 볼의 속도와 질량의 곱셈 곱이 될 것입니다.,
수학의 관점에서,벡터는 정의 가능한 크기 및 방향을 갖는 임의의 객체이다. 벡터는 표준 선이나 모양과 같지 않으므로 몇 가지 특수 수식을 사용하여 그 사이의 각도를 찾아야합니다.
에 대한 공식 사이의 각도 두 벡터
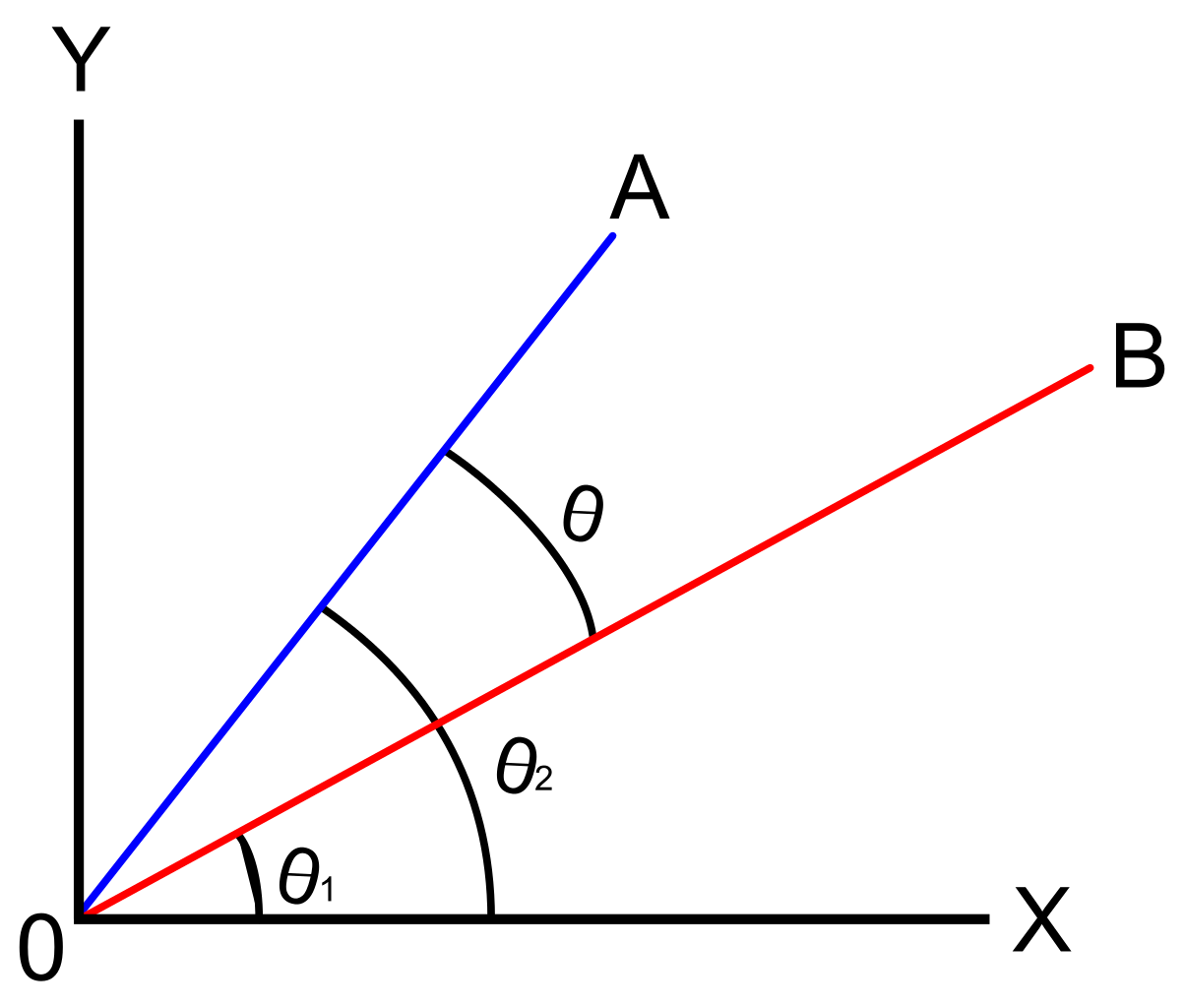
사이의 각도 두 벡터 지연됩니다에 의해 하나의 포인트라고 가장 짧은 각도에서는 우리가 돌아서 하나의 벡터의 위치 공동 방향으로 다른 벡터입니다.,
벡터의 방향 각도에 대한 논의는 양의 x 축과 관련하여 벡터의 각도를 찾는 데 중점을 둡니다. 이것은 표준 위치에서 두 벡터 사이의 각도에 초점을 맞출 것입니다. 벡터는 초기 점이 원점(0,0)인 경우 표준 위치에 있다고합니다.
두 벡터가 a 와 b 로 가정되면 생성 된 점은 a 로 정의됩니다.비.이 두 벡터를 각도\(\세타\)로 구분한다고 가정 해 보겠습니다. 무엇을 알고 각도 측정은 우리가 해결할 것이 도움으로의 수식어:
우리가 알고 있는 점 제품:
\(\vec{a}.,\vec{b}=|\vec{a}||\vec{b}|cos\타\)
이제 사이의 각도 두 벡터 공식은 다음과 같습니다.
\(\타=cos^{-1}\frac{\vec{a}.여기서\\(세타\)는 a 와 b 벡터 사이의 각도입니다.
예를 해결에 대한 각도 사이에 두 개의 벡터 공식
Q.1:산 사이의 각도 두 벡터 3i+4j–k 와 2i–j+k.
솔루션:하자
a=3i+4j–k 와
b=2–j+k
우리는 우리 정의 도로 제품:
니다.b=(3i+4j–k).(2i-j+k)
















답글 남기기