점 제품

벡터의 크기는(그것이 얼마나 오래입니다)방향:

여기에는 두 벡터:

그들은 배가 될 수 있다”를 사용하여 점의 제품”(도 십자가 제품).,

우리가 계산할 수 있습 점의 제품이 두 개의 벡터를 이 방법:

a·b=|a|×|b|×cos(θ)

곳:
|a|은 크기(길이) 벡터의
|b|은 크기(길이)벡터의 b
θ 사이의 각 a 와 b

그래서 우리는 곱의 길이는 시간의 길이 b,다음을 곱하여 코사인의 사이의 각도 및 b

또는 우리가 계산할 수 있습니다 그것은 이 방법:

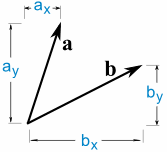
a·b=ax×bx+ay×에 의해

그래서 우리는 곱 x,곱 y,다음을 추가한다.,

두 가지 방법 모두 작동합니다!그 결과는 숫자입니다(“스칼라”라고 불리우므로 벡터가 아니라는 것을 알고 있습니다).

참고:당신은 벡터 Calculatorto 당신을 도울 수 있습니다.

왜 cos(θ)입니까?

좋아,두 벡터를 곱하려면 길이를 함께 곱하는 것이 합리적이지만 같은 방향을 가리킬 때만 가능합니다.,

그래서 우리는 하나”점에서 같은 방향으로”다른 곱하여 cos(θ):


우리는 구성 요소의 는 거짓말과 함께 b		같이 빛나는 빛을 보 는 그림자 속

그리고 우리는 곱!,

두 벡터가 서로 직각 일 때 도트 곱은 0 입니다.이것은 두 벡터가 직각인지 알아내는 편리한 방법 일 수 있습니다.

이 모든 것은 3 개(또는 그 이상)차원에서도 잘 작동합니다. 실제로 매우 유용 할 수 있습니다!

그런 계산을 한 번 시도했지만 각도와 거리에서 모두 작동했습니다… 그것은 매우 힘들었고,삼각법을 많이 포함 시켰고,내 두뇌가 상처를 입었습니다. 위의 방법은 훨씬 쉽습니다.,

점 제품은 스칼라(일반 숫자)대답을 제공하며 때로는 스칼라 곱(scalar product)이라고도합니다.

그러나 벡터를 답으로 제공하는 교차 제품도 있으며 때로는 벡터 제품이라고도합니다.