삼각형의 각도가 180 도까지 더해지지 않을 때

1. 소개

삼각형의 각도가 최대 180 도 또는$\pi$라디안을 추가합니까? 대답은’때로는 예,때로는 아니오’입니다. 이것이 중요한 질문입니까? 예,다른 공리 또는’기하학 게임의 규칙’에 따라 다른 기하학이 있다는 이해로 이어지기 때문입니다. 의미있는 질문입니까? 글쎄,적어도 우리가’angle’과’triangle’이라는 단어의 의미에 동의 할 때까지는 게임의 규칙을 알기 전까지는 아닙니다., 이 문서는 간단히 논의 기본 원칙과를 증명하는 각도의 합의에 삼각형 표면 단위의 영역은 동일하지 않$\pi$지만$\pi 플러스 지역의 삼각형이다. 우리는 단위 구의 표면의 면적이$4\pi$라는 사실을 사용해야한다.<피>2. 큰 정리

전에 우리가 무슨 말을 할 수 있습니다 삼각형은 우리에 동의해야 우리는 무엇을 의미하는 포인트 라인. 우리는 구형 기하학(문자 그대로 구의 표면에있는 기하학)을 연구하고 있습니다., 에서는 이러한 기하학적 공간은 구체의 표면;점은 포인트에서는 표면의 라인의 두 점 사이의 최단 거리입니다 위대한 원형을 포함하는 두 개의 포인트입니다. 큰 원(같은적도체)는 구를 두 개의 동일한 반구로 자릅니다. 이 기하학은 지구상의 장소와 항공 경로 사이의 거리에 대한 명백한 적용을 가지고 있습니다.,

회전하는 영역을 보여주는 훌륭한 원형

각도 사이에 두 개의 중대한 원형에서점 P 유클리드 사이의 각도 방향의 원(거나 엄격하게 사이의 접선하에 있는 원 P). 이 제공에 어려움이에서 탐색기 때문에 지구의 특정 시점에 우리가 생각하는 각도의 두 방향으로 경우에는 지구는 평면했습니다.

룬(lune)은 반포달 지점에서 만나는 두 개의 큰 원에 의해 경계 지어지는 구 표면의 일부입니다., 우리는 먼저 룬의 면적을 고려한 다음 룬을 삼각형으로 나누는 또 다른 위대한 원을 소개합니다.

4 개의 lunes 를 보여주는 회전 구

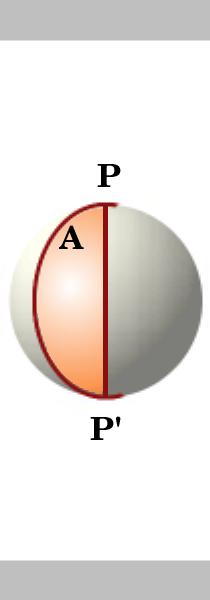
Lemma.

지역의 룬 원 단위의 반경은 두 번의 각,는 경우에는 각도의 룬은 다음의 영역 2A. 두 개의 큰 원형 교차에서 요 점 P P’나누어 영역으로 4 런. 단위 구의 표면 면적은$4\pi$입니다.,

지역의 다음달에 비례하여 그들의 각도에 따라서 이 지역의 룬으로 각 A

${\frac{A}{2\pi}\회{4\pi}={2A}}$

1 운동.

다른 3 개의 lunes 의 영역은 무엇입니까? 당신의 4 지역은$4\파이$까지 추가합니까?

여기에서 답변을 확인하십시오.

삼각형 ABC 의 측면은 실제로 구의 표면을 8 개의 구형 삼각형으로 자르는 3 개의 큰 원의 세그먼트입니다. 점 A 를 통해 두 개의 큰 원 사이에는 네 개의 각도가 있습니다., 우리는 라벨이 각도가 안에 삼각형으로 각도는, 와 마찬가지로 다른 각도의 삼각형으로 각 B 고 각 C.

회전하는 영역을 보여주는 8 개의 삼각형

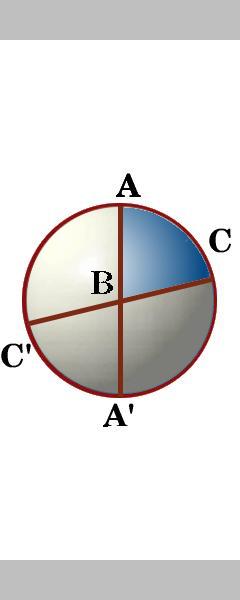
운동 2

회전 영역의 이름을 지정할 수 있습니다 여덟 개의 삼각형이 말하는지 여부를 들어 같은 영역? 여기에서 답변을 확인하십시오.

정리.

각도 A,B 및 C 가있는 단위 구에서 구형 삼각형 ABC 를 고려한 다음 삼각형 ABC 의 면적은

A+B+C-$\pi$입니다.,

다이어그램은 AC 를 통과하는 선을 경계로 한 반구를 내려다 보는 뷰를 보여줍니다. 영역 1 과 영역 3 으로 표시된 영역은 각도가 A 와 c 인 lunes 입니다. B 와 B’를 통해 lunes 를 고려하십시오. 삼각형은각적으로 삼각형 A’B’c 므로 넥타이 모양의 회색 영역,표시된 영역 2,의 합의 영역 삼각형 ABC 및 ‘BC’은 다음과 같습니다 thearea 의 룬 각을 가진 B,같은 2B.,

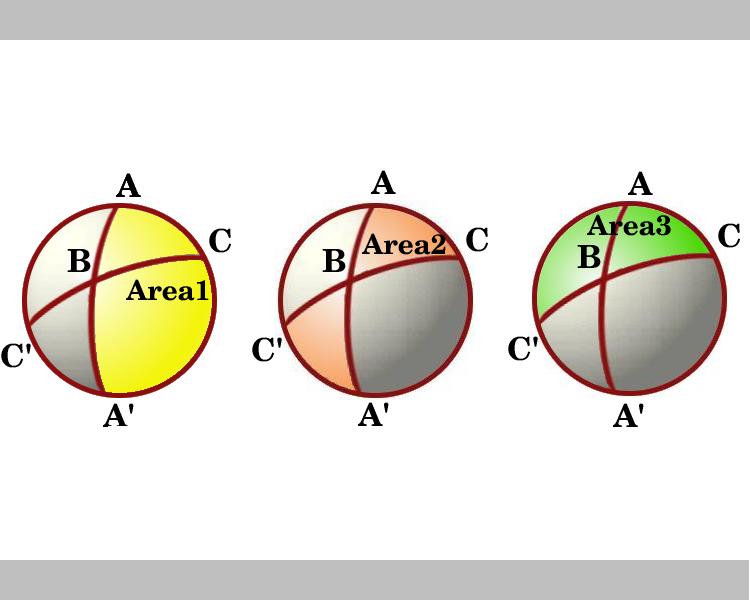
도록 다이어그램에서 우리는 지역의 세 가지런을 사용하여 lemma,이들은:

지역 1=2A
2=2B
지역 3=2C

에 추가 이러한 세 가지 영역을 포함하는 지역의 삼각형의 세 번입니다., Hence

3., Non-유클리드 기하학

때로는 혁신적인 발견은 아무것도 더 이상 실제로 보고되었습니다 무엇에서 우리의 코니다. 이것은 19 세기에 비 유클리드 기하학의 발견 이상의 경우였다. 일부 2000 년 후 유클리드의’요’에 325BC 사람들이 증명하려고 병렬 공준으로 정리된 기하학에서 다른 원칙이지만 실패하고 입 긴 이야기입니다., 한편 수학자들이 사용하던 둥근 형상 모든 시간,형상을 따르는 다른 공리의 유클리드 기하학과 많이 포함되어의 정리,하지만에서는 평행 공준을 유지하지 않습니다. 모두 함께 그들은 코 아래에 비 유클리드 기하학의 예를 가지고있었습니다.

L 에없는 선 L 과 점 P 를 생각해보십시오.큰 질문은”L 과 평행 한 P 를 통해 얼마나 많은 선을 그릴 수 있습니까?”유클리드 기하학에서 대답은”정확히 하나”이며 이것은 평행 가정 의 한 버전입니다., 는 경우 각도의 합의에 삼각형의 기하학은$\pi$라디안 다음에 평행 공준을 보유하고 그 반대의 경우,두 속성은 동일합니다.

에서 구형,기하학의 기본 원칙 우리는 우리 가정(규칙의 게임)에서 다른 유클리드 기하학-이것은 비 유클리드 기하학. 우리가 볼 수있는 둥근 형상 각도의 삼각지 않을 추가하$\pi$라디안 그래서 우리는 우리 것이라 기대하지 않는 병렬 공준을 개최한다., 구형 기하학에서 직선(최단 거리 또는 측지선의 선)은 큰 원이며 기하학의 모든 선은 두 점에서 다른 모든 선을 자릅니다. Parallels 에 대한 큰 질문에 대한 답은”l 에 선 L 과 점 P 가없는 경우 선 L 과 평행 한 P 를 통과하는 선이 없습니다.,”

그리스 수학자(예를 들어 프톨레마이오스의 c150)계산된 측정을 권리의 각 구형 삼각형과 함께 일한 수식의 둥근 삼각법과 아랍에 수학자(예를 들어 자비르 이븐 Aflah c1125 및 Nasir ed din c1250)확장 작업습니다. 이 기사에서 논의 된 공식은 1603 년 Harriot 에 의해 발견되었으며 1629 년 Girard 에 의해 출판되었습니다. 이 주제에 대한 자세한 내용은 Saccerhi(1667-1733)에 의해 개발되었습니다.,

모든 이 크게 유엔에 의해 발견은 19 세기에 발견한의 쌍곡선 형상이 아닌 다른 유클리드 기하학는 병렬 공준을 유지하지 않습니다. 에 둥근 형상(또는 타원 형상)각도는 삼각형의 것보다 더$\pi$라디안과에서 과장되는 형상의 삼각형 추가 less than$\pi$라디안입니다.

추가 독서는 Alan Beardon 의 기사’얼마나 많은 기하학이 있습니까?’그리고 Keith Carne’Strange Geometries’의 기사., 거기에 몇 가지 실용적인 활동을 시도할 수 있습니다 자신을 위해 탐구하는 이러한 형상을 추가하기에 발견될http://nrich.maths.org/MOTIVATE/conf8/index.html