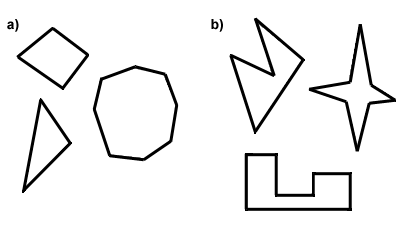
볼록하고 오목한 다각형

매각형 중 하나 볼록 또는 오목. 볼록한 다각형 및 오목한 다각형 사이의 차이는 각도의 측정에 있습니다. 다각형이 되려면벡스,모든 내부 각도는 180 도 미만이어야합니다. 그렇지 않으면 다각형은콘케이브. 다른 방법으로 생각하고 그것은이 대각선의 convexpolygon 모두에서 다각형의 내부는 반면,특정 사선의 오목한 다각형을 것이 거짓말 밖에서 다각형,그 외관입니다., Below in Part A are some convex polygons, and in Part B, some concave polygons. In the rest of this text, you can assume that every polygon discussed is convex.

Figure %: Convex and concave polygons

Regular Polygons

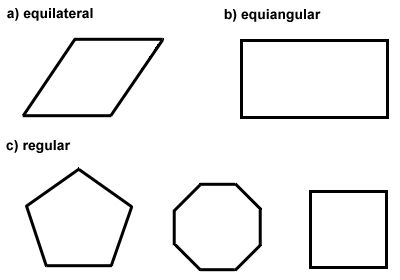
Polygons can also be classified as equilateral, equiangular, or both. Equilateral polygons have congruent sides, like a rhombus. Equiangular polygons have congruent interior angles, like a rectangle., 다각형이 등변과 등변 일 때이를 정다각형이라고합니다. 정사각형은 정다각형의 예입니다. 정다각형의 중심은 다각형의 모든 꼭지점이 등거리 인 지점입니다. 규칙적인 다각형은 다음 섹션에서 살펴볼 특별한 속성을 가지고 있습니다. 다음은 등변,등변 및 규칙적인 다각형의 몇 가지 예입니다.,

Figure %: Equilateral, equiangular, and regular polygons

Congruent Polygons

One more note on polygons: Polygons whose sides are all congruent are congruent polygons. Knowing this term will be important later. In congruent polygons, every segment is congruent.