에 대한 확률이 압연 두 개의 주사위를 가진 여섯면 dotssuch1,2,3,4,5,6 점에서 각각의 죽습니다.

경우 두 개의 주사위를 던진,동시에 따라서 숫자의 이벤트가 될 수 있습니다 62=36 기 때문에 죽을 각각은 1~6 번호에 얼굴입니다. 그런 다음 가능한 결과가 아래 표에 나와 있습니다.,
확률 샘플의 공간을 위한 두 개의 주사위(결과):
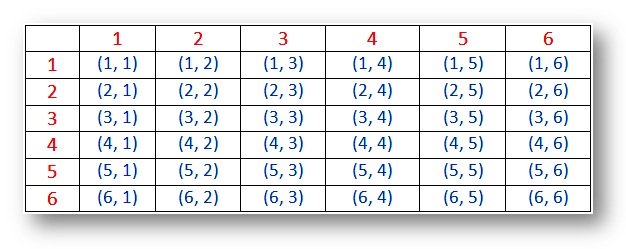
참고:
(i)결과(1, 1), (2, 2), (3, 3), (4, 4), (5, 5) 고(6,6)이라는 남자.쌍(1,2)과(2,1)은 다른 결과입니다.
두 개의 주사위를 굴리는 확률과 관련된 문제:
1. 두 개의 주사위가 굴러갑니다. A,B,C 는 각각 2 의 합계,3 의 합계 및 4 의 합계를 얻는 이벤트가되도록하십시오., 그런 다음,표시하는
(i)간단한 이벤트
(ii)B 및 C 는 화합물 이벤트
(iii)A 와 B 의 상호 배타적인
솔루션:
명확하게,우리
A={(1,1)}, B= {(1, 2), (2, 1)} C= {(1, 3), (3, 1), (2, 2)}.A 는 단일 샘플 포인트로 구성되므로 간단한 이벤트입니다.
(ii)B 와 C 는 둘 이상의 샘플 포인트를 포함하므로 각 샘플 포인트는 복합 이벤트입니다.
(iii)A∩B=∅이므로 A 와 B 는 상호 배타적입니다.
2. 두 개의 주사위가 굴러갑니다., A 는 두 개의 주사위에 표시된 숫자의 합이 5 인 이벤트이고 B 는 주사위 중 적어도 하나가 a3 을 표시하는 이벤트입니다.
두 사건(i)은 상호 배타적인가,(ii)철저한가? 당신의 대답을 뒷받침하는 논쟁을하십시오.
솔루션:
두 개의 주사위를 굴릴 때 n(S) = (6 × 6) = 36.
지금= {(1, 4), (2, 3), (4, 1), (3, 2)}, 그리고
B= {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1,3), (2, 3), (4, 3), (5, 3), (6, 3)}
(i)∩B= {(2, 3), (3, 2)} ≠ ∅.따라서 A 와 B 는 상호 배타적이지 않습니다.,
(ii)또한 A∪B≠S.
따라서 a 와 B 는 철저한 이벤트가 아닙니다.
더 많은 예제와 관련된 질문에 대한 확률을 던지고 두 개의 주사위입니다.
3. 두 개의 주사위가 동시에 던져집니다.,)을 받고 이중
(v)을 받고 합의 8
(vi)을 받고 합 로 나눌 수 있 5
(vii)을 얻어야 합 11
(viii)얻는 여러 개의 3 으로 합계
(ix) 전 적어도 10
(x)을 받고 심지어는 번호로 합계
(xi)을 받고 소수의 합으로
(xii)얻는 이중의 짝
(xiii) 점점 다수의 2 중 하나에 죽고 여러의 3 에 죽습니다.
솔루션:
두 개의 서로 다른 주사위를 던진되고 동시에 수 1,2,3,4,5,6 에 그들의 얼굴입니다., 우리는 두 개의 다른 주사위를 던진 단일 주사위에서 가능한 결과의 총 수가(6×6)=36 임을 알고 있습니다.
(i)제품으로 6 을 얻는 것:
Let E1=제품으로 6 을 얻는 이벤트. 수은 누구의 제품이 될 것입니다 E1==4
그러므로,확률 ofgetting’여섯 개의 제품으로’
번호 유리한 결과
P(E1)=총 수의 가능한 결과
=4/36
=1/9
(ii)을 받고 합≤3:
자 E2=이벤트의을 받고 합≤3., 숫자의 합을≤3 될 것입니다 E2==3
그러므로,확률 ofgetting 합≤3′
번호 유리한 결과
P(E2)=총 수의 가능한 결과
=3/36
=1/12
(iii)을 받고 합≤10:
자 E3=이벤트의을 받고 합≤10. 숫자의 합을≤10E3=
=33
그러므로,확률 ofgetting 합≤10′
번호 유리한 결과
P(E3)=총 수의 가능한 결과
=33/36
=11/12
(iv)을 받고 이중:하자 E4=이벤트의 점점 더블릿입니다., 수있는 더블릿 될 것입니다 E4==6
그러므로,확률 ofgetting’이중’
번호 유리한 결과
P(E4)=총 수의 가능한 결과
=6/36
=1/6
(v)을 받고 합의 8:
자 E5=이벤트의 합의 8. 수은 합의 8 될 것입니다 E5==5
그러므로,확률 ofgetting’의 합 8′
번호 유리한 결과
P(E5)=총 수의 가능한 결과
=5/36
(vi)을 받고 합 로 나눌 수 있 5:
자 E6=이벤트 얻기의 합계 나눌에 의해 5., 숫자의 합을 나눌에 의해 5E6==7
그러므로,확률 ofgetting’합계 나눌하여 5′
번호 유리한 결과
P(E6)=총 수의 가능한 결과
=7/36
(vii)을 얻어야 합 11:
자 E7=이벤트의를 얻어야 합 11. 이벤트의 합계 리뷰 11 될 것입니다 E7==3
그러므로,확률 ofgetting’의 합계 리뷰 11′
번호 유리한 결과
P(E7)=총 수의 가능한 결과
=3/36
=1/12
(viii)를 얻으로 중단하지 않 3 으로 합니다.
자 E8=이벤트의 여러의 3 으로 합니다., 의 이벤트가 다수의 3 으로 합 E8==12
그러므로,확률 ofgetting’다수의 3 의 합으로’
번호 유리한 결과
P(E8)=총 수의 가능한 결과
=12/36
=1/3
(ix)을 받고 totalof 어야 10:
자 E9=이벤트의 점점 적어도 총 10., 의 이벤트는 적어도 총 10E9==6
그러므로,확률 ofgetting’의 총 적어도 10′
번호 유리한 결과
P(E9)=총 수의 가능한 결과
=6/36
=1/6
(x)을 받고 evennumber 으로 합니다.
자 E10=이벤트의 수도로 합니다., 이벤트의 번호로 합 E10==18
그러므로,확률 ofgetting’짝수로 합계
번호 유리한 결과
P(E10)=총 수의 가능한 결과
=18/36
=1/2
(xi)을 받고 primenumber 으로 합니다.
자 E11=의 이벤트를 받고 소수의 합으로., 이벤트는 소수의 합으로 될 것입니다 E11==15
그러므로,확률 ofgetting’소수의 합으로’
번호 유리한 결과
P(E11)=총 수의 가능한 결과
=15/36
=5/12
(xii)을 받고 adoublet 의 숫자:
자 E12=이벤트의 점점 더블릿의 숫자입니다., 의 이벤트는 이중의 짝을 것입 E12==3
그러므로,확률 ofgetting’이중의 짝’
번호 유리한 결과
P(E12)=총 수의 가능한 결과
=3/36
=1/12
(xiii)를 얻으로 중단하지 않 2 중 하나에 죽고 여러의 3 에 죽습니다:
자 E13=이벤트의 여러의 2 중 하나에 죽고 여러의 3 에 죽습니다., 의 이벤트가 다수의 2 중 하나에 죽고 여러의 3 에서 다른 다이 될 것입니다 E13==11
그러므로,확률 ofgetting’다수의 2 중 하나에 죽고 여러의 3 에서 다른 다이’
번호 유리한 결과
P(E13)=총 수의 가능한 결과
=11/36
4. 두 가지가 던져집니다. (I)합계 5 를 얻는 것에 찬성하여 확률을 찾고(ii)합계 6 을 얻는 것에 반대하는 확률을 찾으십시오.
해결책:
우리는 두 개의 다이 중 하나의 던진에서 가능한 결과의 총 수는(6×6)=36 임을 알고 있습니다.
s 가 샘플 공간이되도록하십시오. 그런 다음 n(S)=36 입니다.,
(i)합계 5 를 얻는 것에 찬성하는 확률:
e1 이 합계 5 를 얻는 이벤트가되도록하십시오. 그런 다음
E1= {(1, 4), (2, 3), (3, 2), (4, 1)}
⇒P(E1)=4
따라서,P(E1)=n(E1)/n(S)=4/36=1/9
⇒확률을 부탁에의 E1=P(E1)/ = (1/9)/(1 – 1/9) = 1/8.
(ii)합계 6 을 얻는 것에 대한 확률:
e2 가 합계 6 을 얻는 이벤트가되도록하십시오. 그런 다음
E2= {(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)}
⇒P(E2)=5
따라서,P(E2)=n(E2)/n(S)=5/36
⇒대한 확률 E2=/P(E2) = (1 – 5/36)/(5/36) = 31/5.
5., 두 개의 주사위,하나는 파란색과 하나의 주황색이 동시에 굴러갑니다.
(i)둘 다
(ii)합이 9 인 두 숫자에서 동일한 숫자를 얻을 확률을 찾습니다.,
솔루션:
가능한 결과는
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
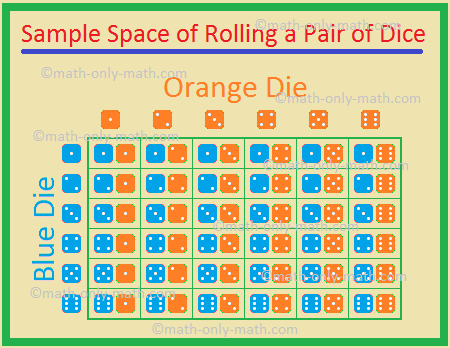
그러므로,총 수의 가능한 결과를=36.,
(i)이벤트에 대한 유리한 결과의 수 E
=두 주사위에서 동일한 숫자를 갖는 결과의 수
=6.
그 정의에 의하여,P(E)=\(\frac{6}{36}\)
=\(\frac{1}{6}\)
(ii) 의 숫자를 호의를 베푸는 결과에 대한 이벤트 F
=숫자의 결과에서는 두 번호에 나타나는 그 합이 9
=4.따라서 정의상 P(F)=\(\frac{4}{36}\)<피>=\(\frac{1}{9}\).
이 예제는 두 개의 주사위를 굴릴 확률에 따라 다른 유형의 문제를 해결하는 데 도움이됩니다.,p>Probability and Playing Cards
Probability for Rolling Two Dice
Solved Probability Problems
Probability for Rolling Three Dice
9th Grade Math
From Probability for Rolling Two Dice to HOME PAGE
















답글 남기기