三角形図角度-サイド角度(ASA)
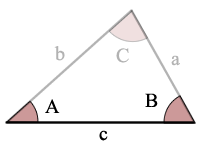
A=角度A
B=角度B
C=角度C
a=辺a
b=辺b
c=辺c
P=周囲
s=半周
k=面積
r=内接する半径円
r=外接円の半径
電卓の使用
以下に示す各計算オプションには、三角形の角度の合計、サインの法則、余弦の法則など、未知の角度と辺の値を解くために、この電卓で使用される方法のシーケンスをリストするサブ箇条書きがあります。, これらのタイプの問題を解決するために使用できる唯一のシーケンスではありません。
- これらの三角法計算機も参照してください:
- 余弦の法則電卓
- サインの法則電卓
三角定理を解く
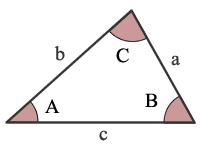
AAAは角度、角度、角度です
三角形は一つの三角形を一意に識別しません。 したがって、トリングルの二つの角度を指定すると、第三の角度のみを計算することができます。,
三角形の2つの角度のサイズを考えると、第三の角度のサイズを計算することができます。 合計は180°または½ラジアンに等しくなります。
C=180°-A-B(度単位)
C=θ-A-B(ラジアン単位)
AAS is Angle,Angle,Side
与えられた角度の2つの角度と1つの辺のサイズを考えると、残りの1つの角度と2つの辺のサイズを計算することができます。
角度の合計ルールを使用して他の角度を見つけ、次に
サインの法則を使用して他の両側のそれぞれを解きます。,
ASAはAngle、Side、Angle
2つの角度のサイズとそれらの2つの角度の間にある辺のサイズを考えると、残りの1つの角度と2つの辺のサイズを計算できます。
角度合計ルールを使用して他の角度を見つけ、次に
サインの法則を使用して他の両側のそれぞれを解きます。,
ASS(またはSSA)はAngle、Side、Sideです
2辺のサイズ(aとc where a<c)と、これらの2辺の間にない角度Aのサイズを考えると、次の条件に応じて、残りの1辺と2つの角度のサイズを計算することができるかもしれません。,fコサインは、他の2つの角度のそれぞれについて解決するために
現在の2つの完全なソリューション
例: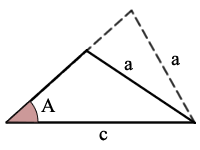
sin(A)=a/c、一つの可能な三角形があります
角度を解くためにサインの法則を使用して、C
他の角度を見つけるために角度のルールの合計を使用して、B
例: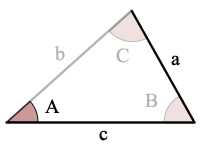
sin(a)>a/c、可能な三角形はありません
エラー通知:sin(a)>a/cだから、解決策はありません。三角形はない!,
例:
SAS is Side,Angle,Side
2つの辺(cとa)のサイズと、それらの2つの辺の間にある角度Bのサイズを考えると、残りの1つの辺と2つの角度のサイズを計算することができます。
残りの辺bを解くために余弦の法則を使用します
どちらの辺aまたはcが最小であるかを決定し、逆の角度AまたはCのサイズを解くために正弦の法則を使用しますそれぞれ。,
角度合計ルールを使用して最後の角度を見つけます
SSSは辺、辺、辺です
3辺のサイズを考えると、三角形の3つの角度すべてのサイズを計算できます。
角度を解くために余弦の法則を使用します。 また、角度合計ルールを使用して、2つの角度がわかったら、最終的な角度を見つけることもできます。,sin-1
余弦の法則
A、bおよびcがそれぞれ角度A、BおよびCとは反対の三角形の脚の長さである場合、余弦の法則は次のようになります。
a2=c2+b2-2bc cos A、cos A、cos A=(b2+c2-a2)/2bc
b2=a2+c2-2ca cos B、cos B、cos B=(c2+a2-b2)/2ca
c2=b2+A2-2ab cos c、cos cについて解く、cos c=(a2+b2-c2)/2ab
たとえば、角度について解く、a=cos-1
その他の三角形の特性
三角周囲、P=a+b+c
三角半周囲、s=0。,5*(a+b+c)
三角形の面積、K=π
三角形の内接円の半径、r=π
三角形の周りの外接円の半径、R=(abc)/(4K)
参考文献/さらに読む
Weisstein、Eric W.”ASS Theorem。”MathWorldから-Wolfram Webリソース。 お尻の定理。
数学は楽しい-SAS三角形を解く
















コメントを残す