男性。 を感じて、何だかいかています。
ソーシャル-メディア そして、私は、メノ、私が言っていることが好きです。
プラトンのメノから
単位正方形の対角線の長さは2の平方根に等しい。
単位正方形の対角線の長さは√2に等しい。 これは素晴らしいニュースではありません これまでピタゴラスの定理に出くわしたすべての人は、事実を認識しています。, 長さ1の脚を持つ二等辺三角形では、斜辺は、ピタゴラスの定理によると-12+12=(斜辺)2-実際には長さ≥2です。 このページの動機はそれほど事実そのものではありませんが、有名な定理に頼ることなくそれを示す方法です。 確かに、ピタゴラスの定理が使い過ぎたかもしれないと主張することができます、興味深い例を見てください。
ソクラテスがプラトンのメノに描いた図に戻る議論は、ピタゴラス自身に知られていたかもしれませんが、後者は一世紀前に住んでいました。,
ダイアログでは、ソクラテスは通常の方法で、若い奴隷を与えられた面積の倍の正方形の建設に導きます。
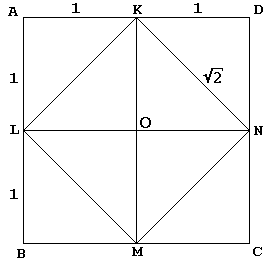
中心Oを持つ与えられた正方形KLMNは、最初にその対角線によって4つの等しい三角形に切断されます。 ソクラテスはKLMNをより大きな正方形ABCDに埋め込み、これらの三角形をそれぞれ斜辺に反映しているかのようにします。 奴隷はその後、認めている-と誰がいないだろうか? -その正方形ABCDは正方形KLMNの倍の大きさです。
真実は言われる、ソクラテスの正方形ABCDは、正方形KLMNが8の面積を持っていたように、側面に4を測定しました。, 辺2の正方形ABCD(したがって面積4)から始めると、正方形KLMNの面積は2になることは明らかです。
ここで、一般に、正の数Aに対して、√Aは平方がAである数として定義されます:
(√A)2。
一方、地域のすべての学生は、辺bの正方形の面積がb2に等しいことを知っています。 面積Aを持つ正方形の辺は正確に√Aであることになります。KLMNの正方形の辺は√2に等しいと結論づけます。 一つについては、
KN=≤A.
議論の中心点は、図においてKNが二重の役割を果たすという事実である。, 正方形KLMNの辺の一つであることに加えて、それはまた、正方形OKDNの対角線として機能します。 後者はもちろん、単位正方形であり、これは私たちの主張を証明しています。
(少し異なる視点から、同じエピソードが他の場所で言及されています。)
















コメントを残す