偶数は、\color{red}2で正確にまたは均等に割ることができる整数です。 数値が\color{red}2で正確に除算されている場合、問題の数値は\color{red}0の除算時に\color{blue}2の残りの部分を持つことを意味します。
精神的な数学を行うことによって、負の数を含む以下の数は、すべてが2で割り切れるために偶数であることは明らかです。,

さらに、多くの学生がゼロは偶数でも奇数でもないと考えていることを指摘したいと思います。
私を信じて、ゼロは同じ単純な理由で偶数とみなされますが、2で割り切れる整数でもあるため、2で割ったときにも余りがありません。 つまり、0\div2=0です。
観測:上記の例から、偶数は常に0、2、4、6、または8の数字で終わることを簡単に一般化することができます。,
しかし、より数学的に正確であるため、偶数を定義するより良い方法があります。 ここにある!
偶数の一般的な形式
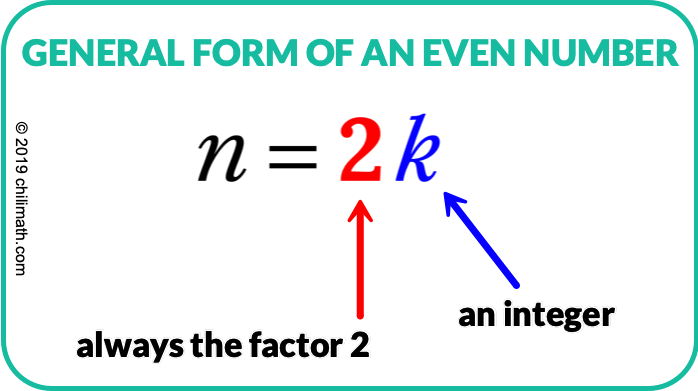
一般的な形式で表現された偶数の例
テストに偶数。 私たちが提示している数学の概念が何であれ、それを検証することが重要です。 それを”math toolbox”に含める前に、何らかの形で私たちにとって意味があるはずです。,
以下は、kが整数であるn=2\、kとして偶数の概念を紹介するいくつかの例です。
\color{red}\LARGE{n=2k}
- 0\to0=2\left(0\right)
- 14\to14=2\left(7\right)
- -32\to-32=2\left({-16}\right)
- 50\to50=2\left({25}\right)
- -78\to-78=2\left({-39}\right)
偶数の要因の一つとしての2の絶え間ない出現は、任意の偶数が実際に2の倍数であることを示唆している。,
あなたも興味があるかもしれません:
奇数とは何ですか?
偶数のリスト
奇数のリスト
















コメントを残す