ベクトルは、方向だけでなく、大きさの両方を持つものを記述するために科学において広く有用である。 それらは通常、尖った矢印の助けを借りて描かれ、その長さはベクトルの大きさを表します。 それは通常どこかダウンフィールドと大きさの方向を持っているので、クォーターバックのパスは簡単な例です。 時には、いくつかのオブジェクトに取り組んで二つのベクトルを このような場合、これらのベクトル間の角度は重要です。, このトピックでは、二つのベクトルの式と例の間の角度について説明します。 私たちはそれを学ぼう!
ベクトルの概念
フィールドオフ、ベクトルは、物理的なオブジェクトや活動の任意の数を表すために使用することができます。 例えば。 たとえば、風はベクトル量です。 それは、どの特定の場所でも、それはマグニチュードと同様に方向を持っているからです。 次に、いくつかの異なる地理的位置の風ベクトルを描画することによって、任意の時点での気流のマップを作成できます。
移動するオブジェクトの多くのプロパティも一種のベクトルです。, にはビリヤードボール、その速度ベクトルを記述します。 これは、ベクトルの矢印マークの方向を動きの方向として示し、ベクトルの長さはボールの速度を表します。
ビリヤードボールの運動量もベクトル量の例です。 それは質量倍速度に等しいので。 したがって、ボールの運動量ベクトルは、その速度ベクトルと同じ方向にポイントします。 そして、運動量ベクトルの大きさは、ボールの速度とその質量の乗算積になります。,
数学の観点から、ベクトルは定義可能な大きさと方向を持つ任意のオブジェクトです。 ベクトルは標準の線や図形と同じではないので、それらの間の角度を見つけるために特別な数式を使用する必要があります。
二つのベクトル間の角度のための式
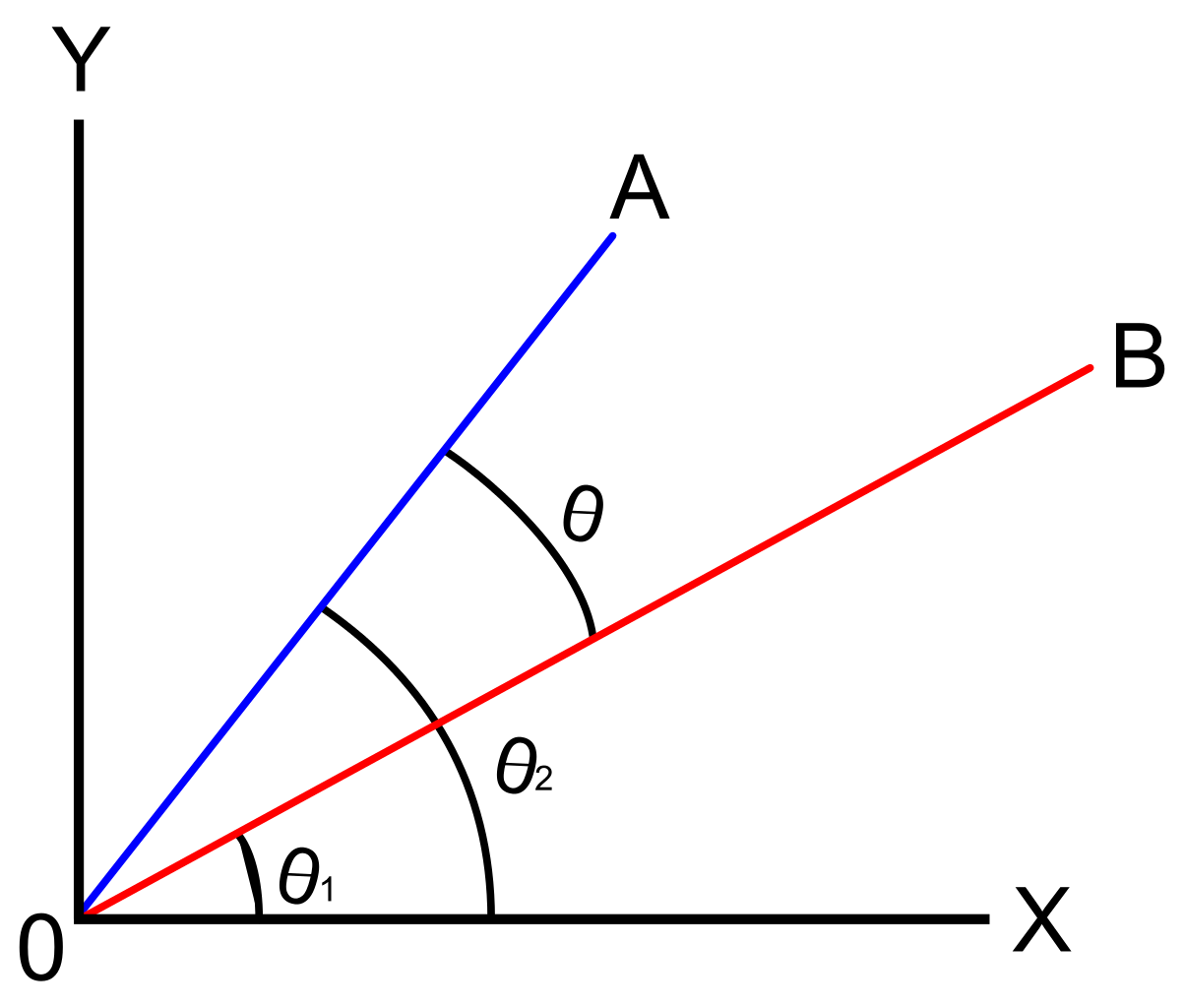
二つのベクトル間の角度は、我々は別のベクトルとの共方向の位置にベクトルの一つを回す必要がある最短角,
ベクトルの方向角に関する議論は、正のx軸に対するベクトルの角度を見つけることに焦点を当てています。 これは、標準位置にある二つのベクトル間の角度に焦点を当てます。 ベクトルは、その初期点が原点(0,0)である場合、標準位置にあると言われます。
二つのベクトルがaとbと仮定される場合、作成されたドットはaとして定義されます。これら二つのベクトルが角度\(\theta\)で区切られていると仮定しましょう。 角度の測定が何であるかを知るために、与えられた式の助けを借りて解決します:
内積を知っています:
\(\vec{a}.,\vec{b}=|\vec{a}||\vec{b}|cos\シータ\)
ここで、二つのベクトル式の間の角度は次のとおりです。
\(\theta=cos^{-1}\frac{\vec{a}。\vec{b}}{|\vec{a}||\vec{b}|}\)
ここで、\(theta\)はaベクトルとbベクトルの間の角度です。
二つのベクトル間の角度のための解決された例式
Q.1:二つのベクトル間の角度を計算します3i+4j–kと2i–j+k。
解:しましょう、
a=3i+4j–kと
b=2i–j+k
我々は、ドット積を次のように定義します。
b=(3i+4j-k)である。(2i-j+k)
















コメントを残す