ドット積

ベクトルは大きさ（どのくらいの長さ）と方向を持ちます。

ここでは二つのベクトルがあります。

“ドット積”を使って乗算することができます（クロス積も参照）。,

我々は、このように二つのベクトルのドット積を計算することができます：

a·b=|a|×|b|×cos（θ）

ここで、
|a|はベクトルaの大きさ（長さ）です
|b|はベクトルbの大きさ（長さ）です
θはまたは、このように計算できます：

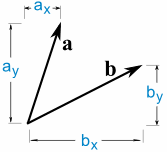
a·b=ax×bx+ay×によって

だから、xを掛け、yを掛けます。を追加します。,

どちらのメソッドも機能します！

そして、結果は数値です（”スカラー”と呼ばれるので、ベクトルではないことがわかります）。

注：あなたはベクトルCalculatortoを使用することができますあなたを助けます。

なぜcos(θ)なのでしょうか？

OK、二つのベクトルを乗算するには、それらの長さを一緒に乗算するのが理にかなっていますが、同じ方向を指している場合にのみ。,したがって、cos（θ）を掛けることによって、一方の”同じ方向のポイント”を他方のポイントとします。


私たちは、bと一緒にあるa のコンポーネントを取ります		見るために光を照らすように影がどこにあるか

その後、我々は乗算します！,

二つのベクトルが互いに直角であるとき、内積はゼロです。

これは、二つのベクトルが直角であるかどうかを調べるための便利な方法です。

これはすべて3つ（またはそれ以上）の次元でも正常に動作します。

そして、実際には非常に便利なことができます！

私は一度そのような計算を試みましたが、すべて角度と距離で機能しました。.. それは非常に難しかった、三角法の多くを関与し、私の脳が傷つきました。上記の方法ははるかに簡単です。,

内積はスカラー（通常の数）の答えを与え、スカラー積と呼ばれることもあります。

しかし、答えとしてベクトルを与えるクロス積もあり、ベクトル積と呼ばれることもあります。