代数II:多項式

多項式の根

関数の根またはゼロは、変数に接続されたとき、関数がゼロに等しくなる数です。 したがって、多項式P(x)の根は、P(x)=0となるようなxの値である。

有理零点定理

有理零点定理は次のように述べています。

有理零点定理を使って多項式のすべての有理零点を見つけることができます。, P>

1. 多項式を降順に並べる
2. 定数項のすべての因子を書き留めます。 これらはすべてpの可能な値です。
3. 先頭の係数のすべての要因を書き留めます。 これらはqのすべての可能な値です。
4. のすべての可能な値を書き留めます。 因子は負になる可能性があるため、と-の両方を含める必要があります。 各値を単純化し、重複をクロスアウトします。,
5. 合成除算を使用して、P()=0のの値を決定します。 これらはすべてP(x)の有理根である。例：P（x）=x3-9x+9+2×4-19×2のすべての有理ゼロを見つけます。

   

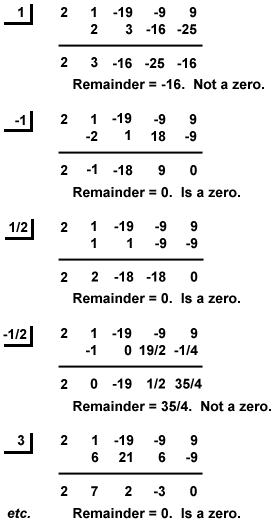
   したがって、P(x)の有理根はx=-3、-1、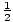、および3である。多項式を因数分解するために有理零点定理をよく使うことができます。, 合成除算を使用して、一つの実根aを見つけることができ、P（x）をx-aで割ったときの商を見つけることができます。 多項式が完全に因数分解されるまで、このプロセスを続けることができます。