モバイル通知を表示すべてのノートを表示すべてのノートを非表示
モバイル通知
あなたは”狭い”画面の幅を持つデバイス上にあるように見えます(つまり、あなたはおそらく携帯電話上にいます)。 このサイト上の数学の性質上、それは風景モードで最高のビューです。 お使いのデバイスがランドスケープモードにない場合、方程式の多くは、お使いのデバイスの側から実行されます(それらを見るためにスクロールすることができるはずです)とメニュー項目の一部が原因狭い画面幅に切断されます。,
セクション4-11:線形近似
このセクションでは、導関数ではなく、関数への接線の適用を見てみましょう。 もちろん、接線を得るためには導関数を取る必要があるので、何らかの形でこれは導関数の適用でもあります。
\
関数とその接線の次のグラフを見てみましょう。
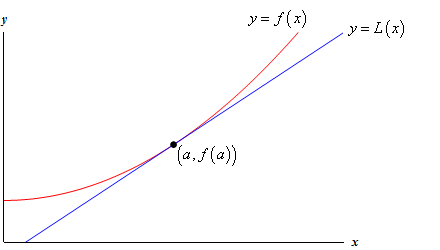
それでは、なぜこれを行うのでしょうか? 例を見てみましょう。,
線形近似は、\(x=a\)の”近く”にとどまる限り、\(f\left(x\right)\)の値を近似するのに非常に良い仕事をします。 しかし、\(x=a\)から遠く離れるほど、近似は悪化しやすくなります。 ここでの主な問題は、良い近似を得るために\(x=a\)にどれだけ近づく必要があるかは、使用している関数と使用している\(x=a\)の値の両方に依存す また、\(x=a\)からどれだけ離れていても”良い”近似を得ることができるかを予測する簡単な方法はないことがよくあります。,
実際にいくつかの場所でかなり頻繁に使用されている別の例を見てみましょう。
これは実際にはやや重要な線形近似です。 光学系では、この線形近似は式を単純化するためによく使用されます。 この線形近似は、振り子の動きや弦の振動を記述するのにも使用されます。
















コメントを残す