1。 はじめに
三角形の角度は180度または$pi$ラジアンになりますか? 答えは”時にははい、時にはいいえ”です。 これは重要な質問ですか? はい、それは異なる公理または”幾何学のゲームのルール”に基づいて異なる形状があることを理解することにつながるからです。 それは意味のある質問ですか? まあいいえ、少なくとも私たちがゲームのルールを知るまで、私たちが”角度”と”三角”という言葉の意味に合意するまではありません。, この記事では、基礎となる公理について簡単に説明し、単位球の表面上の三角形の角度の合計が$\pi$ではなく$\pi$に三角形の面積を加えたものであると 単位球の表面の面積は$4\pi$であるという事実を使用します。
2. 大きな定理
三角形が何であるかを言う前に、点と線によって何を意味するのかに同意する必要があります。 私たちは、球形幾何学(文字通り球の表面上の幾何学)に取り組んでいます。, この幾何学において、空間は球の表面であり、点はその表面上の点であり、二つの点の間の最短距離の線は二つの点を含む大円である。 大きな円(赤道)は、球を二つの等しい半球に切断する。 この幾何学的形状は、地球上の場所と航空経路との間の距離に明らかな応用を有する。,
大円を示す回転球

点Pにおける二つの大円の間の角度は、円の方向の間のユークリッド角度です(または厳密にはpにおける円の接線の間の角度)。 これは、任意の点で地球がその時点で平らであるかのように二つの方向の間の角度を考えるので、地球上の航行には困難をもたらさない。
ルーンは、対蹠点で会う二つの大円によって囲まれた球の表面の一部である。, 最初にluneの面積を検討し、次にluneを三角形に分割する別の大きな円を導入します。
4つのルーンを示す回転球
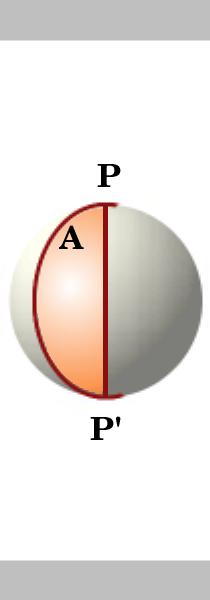
補題。
単位半径の円上のluneの面積はその角度の倍であり、luneの角度がAであり、その面積が2Aである場合、対峰点PとP’で交差する二つの大円は球を4つのルーンに分割する。 単位球の表面の面積は$4\pi$です。,
ルーンの面積はPでの角度に比例するので、角度Aのルーンの面積は
${\frac{A}{2\pi}\times{4\pi}={2A}}$
演習1。
他の3つのルーンの領域は何ですか? あなたの4つの領域は$4\pi$まで加算されますか?
ここであなたの答えを確認してください。
三角形ABCの辺は、実際に球の表面を八つの球面三角形に切断する三つの大円のセグメントです。 点Aを通る二つの大円の間には四つの角度があります。,
8つの三角形を示す回転球
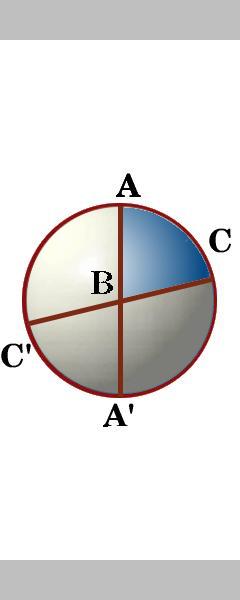
演習2
球の回転あなたは八つの三角形に名前を付け、それらのいずれかが同じ領域を持っているかどうかを言うことができますか? 解答のチェック。
定理。そして、三角形ABCの面積は
A+B+C-$pi$です。,
図は、その境界としてACを通る線を有する半球を見下ろすビューを示しています。 エリア1とエリア3のマークされた領域は、それぞれ角度AとCのルーンです。 BとB’を通してルーンを考えてみましょう。 三角形ABCは三角形A’B’C’と一致するので、三角形ABCとA’BC’の面積の合計である蝶ネクタイ形の影付き領域、マークされた領域2は、角度Bのluneの面積、すなわち2Bに等しい。,
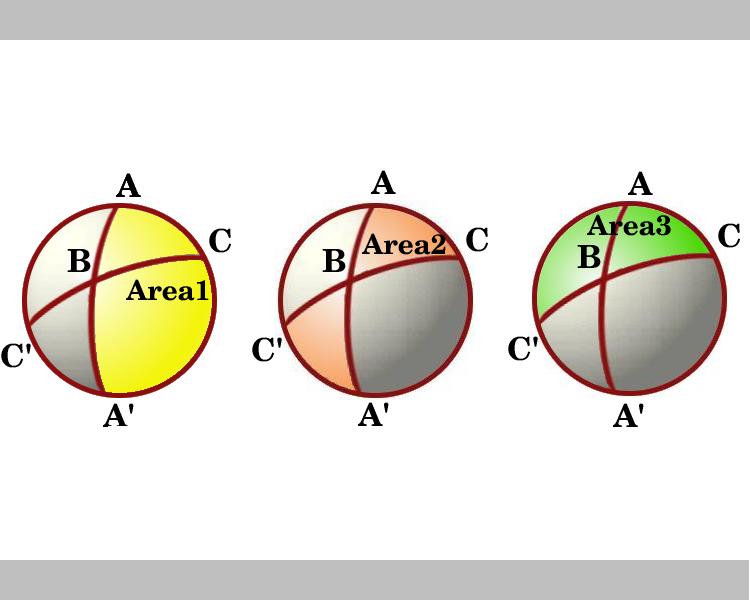
だから、図では、三つのルーンの領域を参照してくださいし、補題を使用して、これらは次のとおりです。
エリア1=2A
エリア2=2B
エリア3=2C
これらの三つの領域を合計するには、三角形ABCの領域を三回includeめます。, Hence
| Area 1 + Area 2 + Area 3 | = | Area of hemisphere +2(Area of triangle ABC) |
|
2A + 2B + 2C
|
=
|
2 $\pi$ + 2(Area of triangle ABC)
|
|
Area of triangle ABC
|
=
|
A + B + C – $\pi$ .
|
3., 非ユークリッド幾何学
時には革命的な発見は、実際に私たちの鼻の下にすべての時間されているものを見る以上のものではありません。 これは、十九世紀における非ユークリッド幾何学の発見に対するケースでした。 ユークリッドが彼の”要素”を書いた後の2000年の間325BC人々は他の公理から幾何学の定理として平行公準を証明しようとしたが、常に失敗し、長い話です。, 一方、数学者は常に球面幾何学を使用していましたが、ユークリッド幾何学の他の公理に従い、同じ定理の多くを含む幾何学ですが、平行公準は成り立 すべてに沿って彼らは彼らの鼻の下で非ユークリッド幾何学の例を持っていた。
L上にない線Lと点Pを考えてみてください。
l上にない線Lと点Pを考えてみてください。
l上にない線Lと点Pを考えて”ユークリッド幾何学では、答えは`正確に一つ”であり、これは平行公準の一つのバージョンです。, ジオメトリ内のすべての三角形の角度の合計が$\pi$ラジアンである場合、平行公準が成り立ち、その逆も同様です。
球面幾何学では、私たちが仮定する基本的な公理(ゲームのルール)はユークリッド幾何学とは異なります-これは非ユークリッド幾何学です。 球形幾何学では、三角形の角度が常に$\pi$ラジアンに加算されるとは限らないので、平行な仮定が成立するとは思わないことがわかりました。, 球面幾何学では、直線(最短距離または測地線の線)は大円であり、幾何学内のすべての線は他のすべての線を二つの点に切断します。 平行線についての大きな質問に対する答えは、`線Lと点PがL上にない場合、線Lに平行なPを通る線はありません。,”
ギリシャの数学者(例えばプトレマイオスc150)は直角球面三角形の測定値を計算し、球面三角法の公式とアラブの数学者(例えばJabir ibn Aflah c1125とNasir ed-din c1250) この記事で議論されている式は、1603年にHarriotによって発見され、1629年にGirardによって出版されました。 さらに、この主題のアイデアはSaccerhi(1667-1733)によって開発されました。,
このすべては、19世紀の双曲幾何学の発見者によって、平行公準が成り立たない別の非ユークリッド幾何学であることにほとんど気付かれていませんでした。 球形幾何学(楕円幾何学とも呼ばれます)では、三角形の角度は$\pi$ラジアン以上になり、双曲線幾何学では三角形の角度は$\pi$ラジアン未満になります。
さらに読むには、Alan Beardonの記事”How many Geometries Are There?”を参照してください。”そして、キース*カーンによる記事”奇妙なジオメトリ”。, これらのジオメトリをさらに探求するために、あなた自身で試すことができるいくつかの実用的な活動がありますhttp://nrich.maths.org/MOTIVATE/conf8/index.html
















コメントを残す